题目内容
10.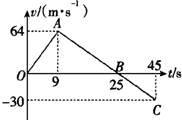 一宇宙空间探测器从某星球表面垂直升高,发动机提供恒力,其质量为M=1500kg,开动一段时间后关闭,根据如图所示v-t图线,求:
一宇宙空间探测器从某星球表面垂直升高,发动机提供恒力,其质量为M=1500kg,开动一段时间后关闭,根据如图所示v-t图线,求:(1)探测器运动情况;
(2)探测器上升的最大高度;
(3)该星球表面重力加速度g的值;
(4)发动机在这一段过程中所做的功.
分析 (1)由速度与时间图象可发现:宇宙空间探测器前9s内向上做匀加速直线运动,9s到25s向上做匀减速直线运动,以后向下做自由落体运动.
(2)探测器上升的最大高度等于三角形OAB的面积大小.
(3)星球表面的重力加速度,即为探测器做自由落体的加速度.所以图象中的9s后的斜率大小就是重力加速度的值.
(4)根据面积求出前9s内物体上升的位移,再由动能定理求发动机做的功.
解答 解:(1)根据题图可知,0-9s内探测器向上做匀加速直线运动,
9-25s内探测器竖直向上做匀减速直线运动,25-45s内探测器做自由落体运动.
(2)探测器上升的最大高度等于三角形OAB的面积大小,则最大高度为:
hm=$\frac{1}{2}$v(t1+t2)=$\frac{1}{2}×$64×25m=800m
(3)A到B匀减速上升的过程中,探测器只受重力作用,则有:
g=$\frac{{v}_{A}-0}{t}$=$\frac{64-0}{25-9}$=4m/s2
(4)在前9s内位移为 x=$\frac{1}{2}×64×9$m=288m
根据动能定理得 W-Mgx=$\frac{1}{2}M{v}_{A}^{2}$
解得 W=7.392×106J
答:(1)分析探测器在各段时间内的运动情况:0-9s内探测器竖直向上做匀加速直线运动,9-25s内探测器竖直向上做匀减速直线运动,25-45s内探测器做自由落体运动;
(2)探测器上升的最大高度800m;
(3)该星球表面的g值4m/s2.
(4)发动机在这一段过程中所做的功是7.392×106J.
点评 本题要学会从图象中寻找信息,知道速度与时间图象的斜率大小即为加速度大小,斜率正负表示加速度的方向,是否是匀加速还是匀减速,哪部分面积表示位移的大小.

练习册系列答案
相关题目
20. 如图所示是单杠运动员做“单臂大回环”的动作简图,质量为60kg的体操运动员,用一只手抓住单杠,伸展身体,以单杠为轴做圆周运动,此过程中,忽略空气阻力,取g=10m/s2,运动员在最低点时手臂受到的拉力可能为( )
如图所示是单杠运动员做“单臂大回环”的动作简图,质量为60kg的体操运动员,用一只手抓住单杠,伸展身体,以单杠为轴做圆周运动,此过程中,忽略空气阻力,取g=10m/s2,运动员在最低点时手臂受到的拉力可能为( )
 如图所示是单杠运动员做“单臂大回环”的动作简图,质量为60kg的体操运动员,用一只手抓住单杠,伸展身体,以单杠为轴做圆周运动,此过程中,忽略空气阻力,取g=10m/s2,运动员在最低点时手臂受到的拉力可能为( )
如图所示是单杠运动员做“单臂大回环”的动作简图,质量为60kg的体操运动员,用一只手抓住单杠,伸展身体,以单杠为轴做圆周运动,此过程中,忽略空气阻力,取g=10m/s2,运动员在最低点时手臂受到的拉力可能为( )| A. | 600N | B. | 2400N | C. | 3000N | D. | 3600N |
1. 原子裂变能够产生巨大的能量,铀原子裂变的链式反应方程为c其中铀的质量为m1,中子质量为m2,钡和氪的质量分别为m3和m4,关于该裂变反应说法正确的是( )
原子裂变能够产生巨大的能量,铀原子裂变的链式反应方程为c其中铀的质量为m1,中子质量为m2,钡和氪的质量分别为m3和m4,关于该裂变反应说法正确的是( )
 原子裂变能够产生巨大的能量,铀原子裂变的链式反应方程为c其中铀的质量为m1,中子质量为m2,钡和氪的质量分别为m3和m4,关于该裂变反应说法正确的是( )
原子裂变能够产生巨大的能量,铀原子裂变的链式反应方程为c其中铀的质量为m1,中子质量为m2,钡和氪的质量分别为m3和m4,关于该裂变反应说法正确的是( )| A. | 链式反应能否发生跟铀原料的体积有关 | |
| B. | 裂变产物钡比铀的比结合能大 | |
| C. | 该方程亏损质量为(m1+m2)-(m3+m4+m2) | |
| D. | 亏损的质量变成能量释放出去 |
18.如图7所示,某人从高出水平地面H的坡上a点以速度v0水平击出一个质量为m的高尔夫球,由于风的影响,球竖直地从洞口b落入洞中,洞深h,落入洞底c瞬间的速度为v,在洞中运动过程中空气阻力忽略不计,以地面为参考面,高尔夫球可看作质点.下列正确的是( )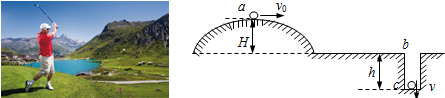

| A. | 高尔夫球落入洞底c时的机械能等于$\frac{1}{2}$mv2-mgh | |
| B. | 高尔夫球落入洞底c时的机械能为mg(H+h)+$\frac{1}{2}$mv02 | |
| C. | 从球被击出至落入洞底过程高尔夫球机械能守恒 | |
| D. | 从球被击出至落入洞口过程减少的重力势能为mgH |
19. 如图所示,是美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道.若“卡西尼”号探测器在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行,环绕n周飞行时间为t,已知引力常量为G,则下列关于土星质量M和平均密度ρ的表达式正确的是( )
如图所示,是美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道.若“卡西尼”号探测器在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行,环绕n周飞行时间为t,已知引力常量为G,则下列关于土星质量M和平均密度ρ的表达式正确的是( )
 如图所示,是美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道.若“卡西尼”号探测器在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行,环绕n周飞行时间为t,已知引力常量为G,则下列关于土星质量M和平均密度ρ的表达式正确的是( )
如图所示,是美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道.若“卡西尼”号探测器在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行,环绕n周飞行时间为t,已知引力常量为G,则下列关于土星质量M和平均密度ρ的表达式正确的是( )| A. | M=$\frac{4{π}^{2}(R+h)^{3}}{G{t}^{2}}$,ρ=$\frac{3π(R+h)^{3}}{G{t}^{2}{R}^{3}}$ | |
| B. | M=$\frac{4{π}^{2}{n}^{2}(R+h)^{2}}{G{t}^{2}}$,ρ=$\frac{3π{n}^{2}(R+h)^{2}}{G{t}^{2}{R}^{3}}$ | |
| C. | M=$\frac{4{π}^{2}{t}^{2}(R+h)^{3}}{G{n}^{2}}$,ρ=$\frac{3π{t}^{2}(R+h)^{3}}{G{n}^{2}{R}^{3}}$ | |
| D. | M=$\frac{4{π}^{2}{n}^{2}(R+h)^{3}}{G{t}^{2}}$,ρ=$\frac{3π{n}^{2}(R+h)^{3}}{G{t}^{2}{R}^{3}}$ |
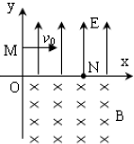 如图所示,在xoy直角坐标平面内,第Ⅰ象限匀强电场沿y轴正方向,第Ⅳ象限匀强磁场垂直于坐标平面向里,质量为m,电量为q的负电粒子,从y轴上的M点(OM=h)以速度v0垂直y轴射入电场,经x轴上的N点(ON=2h)射出电场,进入磁场,最后从y轴上P点(P点未标出)垂直y轴方向射出磁场,不计粒子的重力,求:
如图所示,在xoy直角坐标平面内,第Ⅰ象限匀强电场沿y轴正方向,第Ⅳ象限匀强磁场垂直于坐标平面向里,质量为m,电量为q的负电粒子,从y轴上的M点(OM=h)以速度v0垂直y轴射入电场,经x轴上的N点(ON=2h)射出电场,进入磁场,最后从y轴上P点(P点未标出)垂直y轴方向射出磁场,不计粒子的重力,求:
 在医院里常用如图所示装置对小腿受伤的病人进行牵引治疗.不计滑轮组的摩擦和绳子的质量,绳子下端所挂重物的质量是5kg.问:病人的腿所受水平方向的牵引力是多大?(g=10m/s2)
在医院里常用如图所示装置对小腿受伤的病人进行牵引治疗.不计滑轮组的摩擦和绳子的质量,绳子下端所挂重物的质量是5kg.问:病人的腿所受水平方向的牵引力是多大?(g=10m/s2)