题目内容
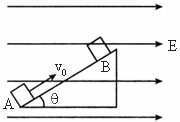
如图所示,把一个倾角为θ的绝缘斜面固定在匀强电场中,电场方向水平向右,电场强度大小为E,有一质量为m、带电荷量为+q的物体以初速度v0,从A端滑上斜面恰好能沿斜面匀速运动,求
(1)物体与斜面间的动摩擦因数.
(2)如果斜面长L,规定A点电势为零,求B点的电势.
(1)物体与斜面间的动摩擦因数.
(2)如果斜面长L,规定A点电势为零,求B点的电势.
分析:(1)物体沿斜面匀速上滑,所受的合外力为零,分析物体的受力情况,根据平衡条件和摩擦力公式求解动摩擦因数.
(2)先根据U=Ed,d是两点沿场强方向的距离求解出AB间的电势差,再求解B点的电势.
(2)先根据U=Ed,d是两点沿场强方向的距离求解出AB间的电势差,再求解B点的电势.
解答: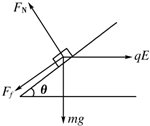 解:(1)物体受力情况如右图所示,将各力沿斜面和垂直斜面两个方向进行正交分解,则根据平衡条件得:
解:(1)物体受力情况如右图所示,将各力沿斜面和垂直斜面两个方向进行正交分解,则根据平衡条件得:
沿斜面方向上:Ff+mgsinθ=qEcosθ ①
垂直斜面方向上:mgcos θ+qEsin θ=FN ②
其中Ff=μFN ③
由①②③得:μ=
.
(2)AB间的电势差为 UAB=ELcosθ
又UAB=φA-φB,φA=0
则得:B点的电势φB=-UAB=-ELcosθ.
答:
(1)物体与斜面间的动摩擦因数为
.
(2)B点的电势为-ELcosθ.
 解:(1)物体受力情况如右图所示,将各力沿斜面和垂直斜面两个方向进行正交分解,则根据平衡条件得:
解:(1)物体受力情况如右图所示,将各力沿斜面和垂直斜面两个方向进行正交分解,则根据平衡条件得:沿斜面方向上:Ff+mgsinθ=qEcosθ ①
垂直斜面方向上:mgcos θ+qEsin θ=FN ②
其中Ff=μFN ③
由①②③得:μ=
| qEcosθ-mgsinθ |
| mgcosθ+qEsinθ |
(2)AB间的电势差为 UAB=ELcosθ
又UAB=φA-φB,φA=0
则得:B点的电势φB=-UAB=-ELcosθ.
答:
(1)物体与斜面间的动摩擦因数为
| qEcosθ-mgsinθ |
| mgcosθ+qEsinθ |
(2)B点的电势为-ELcosθ.
点评:分析受力情况,运用平衡条件处理平衡问题是本题的解题关键.运用公式U=Ed时,要注意d是两点沿场强方向的距离.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
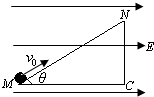 如图所示,把一个倾角为θ高度为h的绝缘斜面固定在匀强电场中,电场方向水平向右,电场强度大小为E,有一质量为m、带电荷量为+q的物体以初速度v0,从M点滑上斜面恰好能沿斜面匀速运动.求
如图所示,把一个倾角为θ高度为h的绝缘斜面固定在匀强电场中,电场方向水平向右,电场强度大小为E,有一质量为m、带电荷量为+q的物体以初速度v0,从M点滑上斜面恰好能沿斜面匀速运动.求 如图所示,把一个物体放在倾角为θ=30°的斜面上,物体受到大小为20N,方向竖直向下的重力作用,但它并不能竖直下落.从力的作用效果看,重力可以分解为两个分力.
如图所示,把一个物体放在倾角为θ=30°的斜面上,物体受到大小为20N,方向竖直向下的重力作用,但它并不能竖直下落.从力的作用效果看,重力可以分解为两个分力.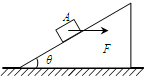 如图所示,把一个重为80N的物体A放在倾角θ=37°的光滑斜面上,并对物体A施加一个水平方向的作用力F.要使物体保持平衡状态,力F的大小为
如图所示,把一个重为80N的物体A放在倾角θ=37°的光滑斜面上,并对物体A施加一个水平方向的作用力F.要使物体保持平衡状态,力F的大小为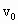 从斜面底端A沿斜面向上运动至B,接着又沿斜面向下运动返回至底端A,此时速度为v,若AB长为L,重力加速度为g.求物体与斜面间动摩擦因数μ.
从斜面底端A沿斜面向上运动至B,接着又沿斜面向下运动返回至底端A,此时速度为v,若AB长为L,重力加速度为g.求物体与斜面间动摩擦因数μ.