题目内容
如图所示，轻绳一端系一小球，另一端固定于O点，在O点正下方的P点钉一颗钉子，使悬线拉紧与竖直方向成一角度θ，然后由静止释放小球，当悬线碰到钉子时，下列说法中不正确的是（ ）分析：当细线碰到钉子瞬间，小球的速度大小不变，而摆长变化，小球碰到钉子后仍做圆周运动，由向心力公式可得出绳子的拉力与小球转动半径的关系；由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系．
解答：解：A、由静止释放小球，当悬线碰到钉子时，由于细线的拉力和重力都与速度方向垂直，不改变速度大小，所以小球的速度大小不变，故A错误．
B、由公式a=
，可知因为摆长变短，导致向心加速度变大，故B正确．
C、由F=ma知，向心力也变大，故C正确．
D、根据牛顿第二定律得：F-mg=m
，F=mg+m
，v不变，r变小，则F变大，故D正确．
本题选错误的，故选：A
B、由公式a=
| v2 |
| r |
C、由F=ma知，向心力也变大，故C正确．
D、根据牛顿第二定律得：F-mg=m
| v2 |
| r |
| v2 |
| r |
本题选错误的，故选：A
点评：解决关键要抓住细线碰到钉子的瞬间，小球的速度大小不变，并要注意细绳碰到钉子前后半径的变化，再由向心力公式分析绳子上的拉力变化．
练习册系列答案
阅读快车系列答案
相关题目
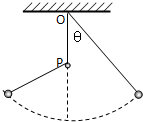如图所示，轻绳一端系一小球，另一端固定于O点，在O点正下方的P点钉一颗钉子，使悬线拉紧与竖直方向成一角度θ，然后由静止释放小球，当悬线碰到钉子时（ ）
（2011?上海模拟）如图所示，轻绳一端系在质量为m的物体A上，另一端与套在粗糙竖直杆MN的轻圆环B相连接．现用水平力F拉住绳子上一点O，使物体A及环B静止在图中虚线所在的位置．现稍微增加力F使O点缓慢地移到实线所示的位置，这一过程中圆环B仍保持在原来位置不动．则此过程中，环对杆摩擦力F1和环对杆的弹力F2的变化情况是（ ）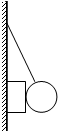
如图所示，轻绳一端系住光滑的球，另一端系在竖直的墙壁上，在墙壁和球之间夹有一矩形物块，物块和球均处于静止．现移走物块并让球靠在墙上不动．下列相关说法正确的是（ ）
如图所示，轻绳一端系在质量为m的物体A上，另一端与套在粗糙竖直杆MN上的轻圆环B相连接．现用水平力F拉住绳子上一点O，使物体A及圆环B静止在图中虚线所在的位置．现稍微增加力F使O点缓慢地移到实线所示的位置，这一过程中圆环B仍保持在原来位置不动．则此过程中，圆环对杆摩擦力F1
（2013?太原一模）如图所示，轻绳一端系在质量为打z的物块A上，另一端系在一个套在粗糙竖直杆MN的圆环B上．现用水平力F拉住绳子上一定点O，使物块A从图中实线位置缓慢下降到虚线位置，但圆环B仍保持在原来位置不动．在这一过程中，下列说法正确的是（ ）