题目内容
14.在一段半径为R=15m的圆弧形水平弯道上,已知弯道路面对汽车轮胎的最大静摩擦力等于车重的μ=0.60倍,则汽车拐弯时的最大速度是3$\sqrt{10}$m/s.分析 汽车拐弯时靠静摩擦力提供向心力,根据牛顿第二定律求出汽车拐弯时的最大速度.
解答 解:根据题意有,汽车拐弯时由地面的摩擦力提供圆周运动的向心力,即:
F=m$\frac{{v}^{2}}{r}$
当摩擦力取最大静摩擦力时,速度最大,则有:
μmg=m$\frac{{v}_{m}^{2}}{r}$
解得vm=$\sqrt{μgR}$=3$\sqrt{10}$m/s,
故答案为:3$\sqrt{10}$.
点评 解决本题的关键知道汽车拐弯时向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.汽车的加速性能是反映汽车性能的重要标志,汽车从一定的初速度加速到一定的末速度,用的时间越少,表明它的加速性能越好.表中是三种型号汽车的加速性能的实验数据,求它们的加速度.
| 汽车型号 | 初速度v0(km•h-1) | 末速度v(km•h-1) | 时间t/s | 加速度a(m•s-2) |
| 某型号高级轿车 | 20 | 50 | 6 | |
| 某型号4t载重汽车 | 20 | 50 | 30 | |
| 某型号10t载重汽车 | 20 | 50 | 60 |
2. 如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )
如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )
 如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )
如图所示的几种情况中,不计绳、弹簧测力计、各滑轮的质量,不计一切摩擦,物体质量都为m,且均处于静止状态,有关角度如图所示.弹簧测力计示数FA、FB、FC、FD由大到小的排列顺序是( )| A. | FB>FD>FA>FC | B. | FD>FC>FB>FA | C. | FD>FB>FA>FC | D. | FC>FD>FB>FA |
6. 用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )
用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )
 用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )
用水平力拉一物体在水平地面上从静止开始做匀加速运动,到t1秒末撤去拉力F,物体做匀减速运动,到t2秒末静止.其速度图象如图所示,且α<β.若拉力F做的功为W,平均功率为P;物体在加速和减速过程中克服摩擦阻力做的功分别为W1和W2,它们的平均功率分别为P1和P2,则下列选项正确的是( )| A. | W=W1+W2 | B. | P<P1+P2 | C. | W1=W2 | D. | P1>P2 |
3. 左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )
左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )
 左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )
左右两个电路都是从左端输入信号,从右端输出信号.图1中输入的是高频、低频混合的交流信号,要求只输出低频信号;图2中输入的是直流和低频交流的混合信号,要求只输出低频交流信号.那么对C1、C2的选择效果最好的是( )| A. | C1用大电容,C2用大电容 | B. | C1用大电容,C2用小电容 | ||
| C. | C1用小电容,C2用大电容 | D. | C1用小电容,C2用小电容 |
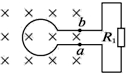 如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=0.2tT,定值电阻R1=6Ω,线圈电阻R2=4Ω.求:
如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=0.2tT,定值电阻R1=6Ω,线圈电阻R2=4Ω.求: 如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=3RB,则三质点的向心加速度之比aA:aB:aC=9:3:1.
如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且RA=RC=3RB,则三质点的向心加速度之比aA:aB:aC=9:3:1. 如图所示,一个质量为m的钢性圆环套在一根固定的足够长的水平直杆上,环的半径略大于杆的半径.环与杆之间的动摩擦因数为μ,t=0时刻给环一个向右的初速度v0,同时对环施加一个方向始终竖直向上的力F,已知力F的大小F=kv(k为常数,v为环的运动速度),且有kv0>mg.t=t1时刻环开始沿杆做匀速直线运动,试求:
如图所示,一个质量为m的钢性圆环套在一根固定的足够长的水平直杆上,环的半径略大于杆的半径.环与杆之间的动摩擦因数为μ,t=0时刻给环一个向右的初速度v0,同时对环施加一个方向始终竖直向上的力F,已知力F的大小F=kv(k为常数,v为环的运动速度),且有kv0>mg.t=t1时刻环开始沿杆做匀速直线运动,试求: