题目内容
如图所示,斜面倾角为θ,高为h.质量为m的小物块从斜面的顶点由静止开始加速滑下,已知物块与斜面间的动摩擦因数为μ.
求(1)物块下滑过程中加速度的大小;
(2)到达斜面底端时速度的大小;
(3)由顶点下滑到底端的过程中,所用的时间.
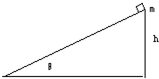
求(1)物块下滑过程中加速度的大小;
(2)到达斜面底端时速度的大小;
(3)由顶点下滑到底端的过程中,所用的时间.

(1)物体下滑过程中受三个力作用,重力,弹力,摩擦力.
其中支持力N=mgcosθ,摩擦力f=μmgcosθ;
由牛顿第二定律得:mgsinθ-μmgcosθ=ma
解得:a=gsinθ-μgcosθ
(2)斜面长度为s=
,由v2=2as
解得:v=
(3)由v=at,得t=
=
答:(1)物块下滑过程中加速度的大小为gsinθ-μgcosθ;
(2)到达斜面底端时速度的大小为
;
(3)由顶点下滑到底端的过程中,所用的时间为
.
其中支持力N=mgcosθ,摩擦力f=μmgcosθ;
由牛顿第二定律得:mgsinθ-μmgcosθ=ma
解得:a=gsinθ-μgcosθ
(2)斜面长度为s=
| h |
| sinθ |
解得:v=
(sinθ-μcosθ)
|
(3)由v=at,得t=
| v |
| a |
| ||
| gsinθ-μgcosθ |
答:(1)物块下滑过程中加速度的大小为gsinθ-μgcosθ;
(2)到达斜面底端时速度的大小为
(sinθ-μcosθ)
|
(3)由顶点下滑到底端的过程中,所用的时间为
| ||
| gsinθ-μgcosθ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (1)在这十个连续的动作中被训航天员处于完全失重状态的时间是多少?
(1)在这十个连续的动作中被训航天员处于完全失重状态的时间是多少?