题目内容
如图所示,在一粗糙水平面上有两个质量均为m的木块1和2,中间用一原长为L、劲度系数为k的轻弹簧连接起来,木块与地面间的动摩擦因数为μ.现用一水平拉力向右拉木块2,当两木块一起以加速度a向右匀加速运动时,求:
(1)两木块之间的距离;
(2)撤去水平拉力瞬间,木块1和2的加速度的大小和方向.
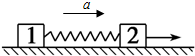
(1)两木块之间的距离;
(2)撤去水平拉力瞬间,木块1和2的加速度的大小和方向.

(1)以木块1为研究对象,
由牛顿第二定律得:kx-μmg=ma ①,
两木块间的距离:s=L+x,
解得:s=L+
;
(2)撤去水平拉力瞬间,木块1的受力情况不变,加速度a1=a,方向向右,
对木块2由牛顿第二定律得:kx+μmg=ma2 ②
由①②解得:a2=2μg+a,方向向左;
答:(1)两木块之间的距离为L+
;
(2)撤去水平拉力瞬间,木块1的加速度大小为a,方向向右,木块2的加速度的大小为2μg+a,方向:向左.
由牛顿第二定律得:kx-μmg=ma ①,
两木块间的距离:s=L+x,
解得:s=L+
| μmg+ma |
| k |
(2)撤去水平拉力瞬间,木块1的受力情况不变,加速度a1=a,方向向右,
对木块2由牛顿第二定律得:kx+μmg=ma2 ②
由①②解得:a2=2μg+a,方向向左;
答:(1)两木块之间的距离为L+
| μmg+ma |
| k |
(2)撤去水平拉力瞬间,木块1的加速度大小为a,方向向右,木块2的加速度的大小为2μg+a,方向:向左.

练习册系列答案
相关题目
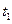 时刻开始进入水面
时刻开始进入水面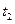 时刻开始进入水面
时刻开始进入水面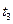 时刻已浮出水面
时刻已浮出水面