题目内容
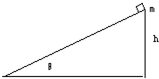
如图所示,某一小车中有一倾角为30°的斜面,当小车沿水平方向向左加速运动时,斜面上的物体m与小车始终保持相对静止,求:
(1)若物体m所受的摩擦力为零,则小车的加速度为多大?
(2)若小车的加速度大小等于重力加速度g,求斜面对物体的摩擦力的大小和方向.

(1)若物体m所受的摩擦力为零,则小车的加速度为多大?
(2)若小车的加速度大小等于重力加速度g,求斜面对物体的摩擦力的大小和方向.

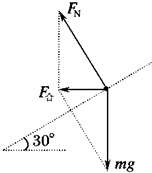
(1)若物体不受摩擦力,受力如图所示,
F=mgtanθ=ma,
解得a=
.
(2)一般情况下m受三个力作用:重力mg,弹力FN,由于给定的加速度大于临界加速度,故斜面对物体的静摩擦力向下.由牛顿第二定律列方程:
FNcos30°-Ffsin30°=mg
FNsin30°+Ffcos30°=ma
得Ff=
mg,方向沿斜面向下.
答:(1)小车的加速度为a=
.
(2)斜面对物体的摩擦力大小为
mg,方向沿斜面向下.
F=mgtanθ=ma,
解得a=
| ||
| 3 |
(2)一般情况下m受三个力作用:重力mg,弹力FN,由于给定的加速度大于临界加速度,故斜面对物体的静摩擦力向下.由牛顿第二定律列方程:
FNcos30°-Ffsin30°=mg
FNsin30°+Ffcos30°=ma
得Ff=
| ||
| 2 |
答:(1)小车的加速度为a=
| ||
| 3 |
(2)斜面对物体的摩擦力大小为
| ||
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目