题目内容
9.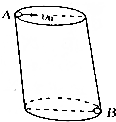 有一上端开口、下端封的内壁光滑的直立圆筒,在底与壁结合处有一小孔,如图所示,在上端口边缘A给小球(其直径略小于小孔直径)一水平初速度v0,沿筒直径方向抛出,正好通过底部小孔B射出(设筒高H,圆筒直径D,球与筒壁碰撞时无能量损失),则下列说法正确的是( )
有一上端开口、下端封的内壁光滑的直立圆筒,在底与壁结合处有一小孔,如图所示,在上端口边缘A给小球(其直径略小于小孔直径)一水平初速度v0,沿筒直径方向抛出,正好通过底部小孔B射出(设筒高H,圆筒直径D,球与筒壁碰撞时无能量损失),则下列说法正确的是( )| A. | 初速度v0一定时D$\sqrt{\frac{g}{2H}}$ | |
| B. | 初速度v0可能是3D$\sqrt{\frac{g}{2H}}$ | |
| C. | 初速度v0可能是4D$\sqrt{\frac{g}{2H}}$ | |
| D. | 初速度v0可以有不同的值,v0越大,小球在圆筒中运动的时间就越短 |
分析 根据高度求出小球运动的时间,结合水平方向上运动的路程,根据运动的时间求出小球的水平初速度.
解答 解:根据H=$\frac{1}{2}g{t}^{2}$得,$t=\sqrt{\frac{2H}{g}}$,
从B点射出,通过水平路程s=(2n+1)D,n=0,1,2,3,…
则初速度${v}_{0}=\frac{(2n+1)D}{t}=(2n+1)D\sqrt{\frac{g}{2H}}$,n=0,1,2,3,…故B正确,A、C错误.
运动的时间由高度决定,与初速度无关,故D错误.
故选:B.
点评 解决本题的关键知道小球在水平方向和竖直方向上的运动规律,抓住等时性,结合运动学公式灵活求解.

练习册系列答案
相关题目
19.某船在一条水流速度一定的河中以恒定的速度渡河,下列说法中正确的是( )
| A. | 船头朝向上游,使船与河岸成某一夹角航行时,有可能使航线最短 | |
| B. | 船头垂直河岸向对岸航行,航行时间最长 | |
| C. | 船头垂直河岸向对岸航行,实际航线最短 | |
| D. | 船头朝向上游,使船与河岸成某一夹角航行时,有可能使航行时间最短 |
20.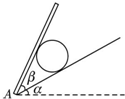 如图所示,一个重力为G的球放在光滑的斜面上,斜面的倾角为α,在斜面上有一光滑的挡板可绕A点转动,用挡板挡住球,使球处于静止状态.若挡板与斜面的夹角β缓慢增大,在此过程中,球对挡板的压力N1和对斜面的压力N2将( )
如图所示,一个重力为G的球放在光滑的斜面上,斜面的倾角为α,在斜面上有一光滑的挡板可绕A点转动,用挡板挡住球,使球处于静止状态.若挡板与斜面的夹角β缓慢增大,在此过程中,球对挡板的压力N1和对斜面的压力N2将( )
 如图所示,一个重力为G的球放在光滑的斜面上,斜面的倾角为α,在斜面上有一光滑的挡板可绕A点转动,用挡板挡住球,使球处于静止状态.若挡板与斜面的夹角β缓慢增大,在此过程中,球对挡板的压力N1和对斜面的压力N2将( )
如图所示,一个重力为G的球放在光滑的斜面上,斜面的倾角为α,在斜面上有一光滑的挡板可绕A点转动,用挡板挡住球,使球处于静止状态.若挡板与斜面的夹角β缓慢增大,在此过程中,球对挡板的压力N1和对斜面的压力N2将( )| A. | N1先减小后增大,N2始终减小 | B. | N1、N2都先减小后增大 | ||
| C. | N1始终减小,N2先减小后增大 | D. | N1和N2都始终增大 |
17. 在水平绝缘地面上放置着质量为m、带电量为+q的物块,在竖直方向上加一个向上的电场,场强E随时间t的变化规律如图所示,不考虑运动过程中受到的空气阻力,重力加速度为g.从t=0开始释放带电物块,在0-4t0时间内( )
在水平绝缘地面上放置着质量为m、带电量为+q的物块,在竖直方向上加一个向上的电场,场强E随时间t的变化规律如图所示,不考虑运动过程中受到的空气阻力,重力加速度为g.从t=0开始释放带电物块,在0-4t0时间内( )
 在水平绝缘地面上放置着质量为m、带电量为+q的物块,在竖直方向上加一个向上的电场,场强E随时间t的变化规律如图所示,不考虑运动过程中受到的空气阻力,重力加速度为g.从t=0开始释放带电物块,在0-4t0时间内( )
在水平绝缘地面上放置着质量为m、带电量为+q的物块,在竖直方向上加一个向上的电场,场强E随时间t的变化规律如图所示,不考虑运动过程中受到的空气阻力,重力加速度为g.从t=0开始释放带电物块,在0-4t0时间内( )| A. | 在t0时刻物块动能最大 | B. | 在2t0时刻物块的重力势能最大 | ||
| C. | 在3t0时刻物块的电势能最小 | D. | 在4t0时刻物块的机械能最大 |
4. 如图所示,物体A、B通过细绳连接在轻滑轮两侧,物体A的质量为B的两倍,开始时用手压住物体B,使物体A静止在距地面高度为h处,放手后物体A下落,B上升的最大高度是( )
如图所示,物体A、B通过细绳连接在轻滑轮两侧,物体A的质量为B的两倍,开始时用手压住物体B,使物体A静止在距地面高度为h处,放手后物体A下落,B上升的最大高度是( )
 如图所示,物体A、B通过细绳连接在轻滑轮两侧,物体A的质量为B的两倍,开始时用手压住物体B,使物体A静止在距地面高度为h处,放手后物体A下落,B上升的最大高度是( )
如图所示,物体A、B通过细绳连接在轻滑轮两侧,物体A的质量为B的两倍,开始时用手压住物体B,使物体A静止在距地面高度为h处,放手后物体A下落,B上升的最大高度是( )| A. | $\frac{h}{3}$ | B. | $\frac{4h}{3}$ | C. | $\frac{5h}{3}$ | D. | 2h |
14.假设一小球在月球上做自由落体运动,第3s内的位移大小为△s,则小球运动的加速度大小为( )
| A. | $\frac{2}{9}$△s | B. | $\frac{9}{2}$△s | C. | $\frac{2}{5}$△s | D. | $\frac{5}{2}$△s |
 如图所示,电荷量为+1×10-6C的点电荷A镶嵌在墙壁上,带电荷量为+3×10-6C的小球B(可视为点电荷)悬挂在长为50cm的轻绳末端,悬点在A的正上方C处,A、C之间的距离为40cm,重力加速度为10m/s2.(已知sin37°=0.6,cos37°=0.8,静电力常量k=9.0×109N•m2/C2)
如图所示,电荷量为+1×10-6C的点电荷A镶嵌在墙壁上,带电荷量为+3×10-6C的小球B(可视为点电荷)悬挂在长为50cm的轻绳末端,悬点在A的正上方C处,A、C之间的距离为40cm,重力加速度为10m/s2.(已知sin37°=0.6,cos37°=0.8,静电力常量k=9.0×109N•m2/C2)