题目内容
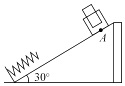
【题目】如图所示,倾角为θ=37°两根平行长直金属导轨的间距为d,其底端接有阻值为R的电阻.整个装置处在垂直斜面向上磁感应强度大小为B的匀强磁场中,质量均为m (质量分布均匀)、电阻均为R的导体杆ab、cd垂直于导轨放置,且与两导轨保持良好接触,两导体杆与导轨的动摩擦因数均为μ=0.5;现杆ab在恒力F作用下沿导轨向上作匀速运动,杆cd能保持静止状态,导轨电阻不计,重力加速度大小为g,求杆ab的速度大小.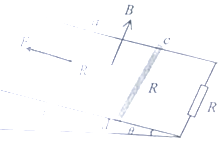
【答案】解:导体杆ab以速度v运动切割磁感线产生感应电动势,则有:E=Bdv,
根据闭合电路的知识有:E= ![]() ,
,
根据并联电路的特点可得通过cd棒的电流强度为 ![]() ,
,
导体杆ab速度较小时,对于导体杆cd则有: ![]() ,
,
解得: ![]() ;
;
导体杆ab速度较大时,对于导体杆cd则有: ![]() ,
,
解得 ![]() ;
;
故导体杆ab的速度应满足条件: ![]() .
.
答:导体杆ab的速度应满足条件为 ![]() .
.
【解析】本题是典型的动电动类型,导体棒切割磁感线,产生感应电动势,首先根据右手定则求出感应电动势大小,再结合闭合电路的知识,求出电流,而导体棒由于有电流,又受到了反向的安培力作用。然后对abb棒的速度进行假设,求初速度的取值范围。
【考点精析】解答此题的关键在于理解电磁感应与力学的相关知识,掌握用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向;求回路中电流强度;分析研究导体受力情况(包含安培力,用左手定则确定其方向);列动力学方程或平衡方程求解.

练习册系列答案
相关题目