题目内容
6.已知地球的半径为R,地面的重力加速度为g,万有引力常量为G,如果不考虑地球自转的影响,那么:(1)求地球的质量表达式
(2)求地球平均密度的表达式
(3)假若不知地球半径和地面重力加速度,但已知近地卫星的运行周期为T,求地球的密度表达式.
分析 由地球表面万有引力等于重力,可得地球质量,再由体积表达式可得地球密度.
人造地球卫星绕地球飞行,靠万有引力提供向心力,表示出地球质量,再求解密度.
解答 解:(1)由地球表面万有引力等于重力,
可得:$\frac{GMm}{{R}^{2}}$=mg
解得:M=$\frac{{gR}^{2}}{G}$
(2)地球体积为:V=$\frac{4}{3}$πR3
故地球密度为:ρ=$\frac{M}{V}$=$\frac{3g}{4πGR}$,
(3)人造地球卫星绕地球飞行,靠万有引力提供向心力,
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
由于是近地卫星,所以r=R,
所以M=$\frac{{{4π}^{2}R}^{3}}{{GT}^{2}}$,
故地球密度为:ρ=$\frac{M}{V}$=$\frac{3π}{{GT}^{2}}$,
答:(1)地球的质量表达式是$\frac{{gR}^{2}}{G}$;
(2)地球平均密度的表达式是$\frac{3g}{4πGR}$,
(3)假若不知地球半径和地面重力加速度,但已知近地卫星的运行周期为T,地球的密度表达式是$\frac{3π}{{GT}^{2}}$.
点评 解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论,并能灵活运用.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
16. 有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图示的平面内,O点为两根导线连线ab的中点,M、N为ab的中垂线上的两点,OM=ON.若两导线中通有大小相等、方向相同的恒定电流(直线电流产生的磁场在某点的磁感应强度B的大小跟该点到通电导线的距离r成反比),则关于线段MN上各点的磁感应强度的说法中正确的是( )
有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图示的平面内,O点为两根导线连线ab的中点,M、N为ab的中垂线上的两点,OM=ON.若两导线中通有大小相等、方向相同的恒定电流(直线电流产生的磁场在某点的磁感应强度B的大小跟该点到通电导线的距离r成反比),则关于线段MN上各点的磁感应强度的说法中正确的是( )
 有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图示的平面内,O点为两根导线连线ab的中点,M、N为ab的中垂线上的两点,OM=ON.若两导线中通有大小相等、方向相同的恒定电流(直线电流产生的磁场在某点的磁感应强度B的大小跟该点到通电导线的距离r成反比),则关于线段MN上各点的磁感应强度的说法中正确的是( )
有两根长直导线a、b互相平行放置,如图所示为垂直于导线的截面图.在图示的平面内,O点为两根导线连线ab的中点,M、N为ab的中垂线上的两点,OM=ON.若两导线中通有大小相等、方向相同的恒定电流(直线电流产生的磁场在某点的磁感应强度B的大小跟该点到通电导线的距离r成反比),则关于线段MN上各点的磁感应强度的说法中正确的是( )| A. | M点和N点的磁感应强度大小相等,方向相同 | |
| B. | M点和N点的磁感应强度大小相等,方向相反 | |
| C. | 在线段MN上各点的磁感应强度都不可能为零 | |
| D. | 若在N点放一小磁针,静止时其北极沿ON指向O点 |
17.关于质点,下列说法正确的是( )
| A. | 只有质量很小的物体才能看成质点 | |
| B. | 研究车轮的转动,可以把车轮看成质点 | |
| C. | 研究体操运动员的动作时,可以把运动员看成质点 | |
| D. | 研究一列火车从重庆开往成都的运行速度时,可以把这列火车看成质点 |
14. 两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )
两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )
 两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )
两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )| A. | 顺时针方向转动,同时靠近导线AB | B. | 逆时针方向转动,同时靠近导线AB | ||
| C. | 逆时针方向转动,同时离开导线AB | D. | 顺时针方向转动,同时离开导线AB |
15.地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
| A. | 物体在赤道处受的地球引力等于两极处,而重力小于两极处 | |
| B. | 赤道处的角速度比北纬45°大 | |
| C. | 地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大 | |
| D. | 地面上的物体随地球自转时提供向心力的是重力 |
 在如图所示电路中,定值电阻R0=2Ω,安培表和伏特表均为理想电表.闭合开关K,当滑动变阻器Rx滑片P从b端移向a端时,发现电压表的电压变化从0V到3V时,安培表从1.0A变化到0.75A.求:
在如图所示电路中,定值电阻R0=2Ω,安培表和伏特表均为理想电表.闭合开关K,当滑动变阻器Rx滑片P从b端移向a端时,发现电压表的电压变化从0V到3V时,安培表从1.0A变化到0.75A.求: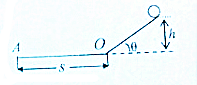 一光滑斜面圆滑地连接着一光滑平面,平面上的A点距斜面底端O为s,斜面倾角为θ如图,一小球从斜面上某处滑下要运动到A点所用时间最短,小球开始运动时所在的高度h为多少?最短时间是多少?
一光滑斜面圆滑地连接着一光滑平面,平面上的A点距斜面底端O为s,斜面倾角为θ如图,一小球从斜面上某处滑下要运动到A点所用时间最短,小球开始运动时所在的高度h为多少?最短时间是多少? 为了“探究气体等温变化的规律”,某学习小组,设计了如下实验,如图所示,用粗细均匀的U型管封闭一定质量的空气,右端开口,可通过右端口添加液体来改变压强,测量左端空气柱长度,来得到不同压强下,空气的体积.已知外界大气压为76cm汞柱高,图中给出了实验中,气体的两个不同的状态.
为了“探究气体等温变化的规律”,某学习小组,设计了如下实验,如图所示,用粗细均匀的U型管封闭一定质量的空气,右端开口,可通过右端口添加液体来改变压强,测量左端空气柱长度,来得到不同压强下,空气的体积.已知外界大气压为76cm汞柱高,图中给出了实验中,气体的两个不同的状态.