题目内容
18.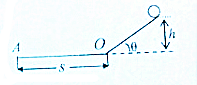 一光滑斜面圆滑地连接着一光滑平面,平面上的A点距斜面底端O为s,斜面倾角为θ如图,一小球从斜面上某处滑下要运动到A点所用时间最短,小球开始运动时所在的高度h为多少?最短时间是多少?
一光滑斜面圆滑地连接着一光滑平面,平面上的A点距斜面底端O为s,斜面倾角为θ如图,一小球从斜面上某处滑下要运动到A点所用时间最短,小球开始运动时所在的高度h为多少?最短时间是多少?
分析 根据牛顿第二定律求出小球在斜面上的加速度,结合运动学公式求出小球在斜面上的运动时间和末速度,从而得出小球在水平面上的运动时间,得出总时间,根据数学不等式知识求出最短时间.
解答 解:小球在斜面上运动的加速度a=gsinθ,
根据$\frac{h}{sinθ}=\frac{1}{2}a{t}^{2}$得:t1=$\sqrt{\frac{2h}{gsi{n}^{2}θ}}=\frac{1}{sinθ}\sqrt{\frac{2h}{g}}$,
到达底端的速度为:v=$\sqrt{2a\frac{h}{sinθ}}=\sqrt{2gh}$,
则在水平面上运动的时为:间${t}_{2}=\frac{s}{v}=\frac{s}{\sqrt{2gh}}$,
运动的时间为:t=${t}_{1}+{t}_{2}=\frac{1}{sinθ}\sqrt{\frac{2h}{g}}+\frac{s}{\sqrt{2gh}}$≥$2\sqrt{\frac{s}{gsinθ}}$,
当$\frac{1}{sinθ}\sqrt{\frac{2h}{g}}=\frac{s}{\sqrt{2gh}}$时,t取最小值,解得:h=$\frac{ssinθ}{2}$,${t}_{min}=2\sqrt{\frac{s}{gsinθ}}$.
答:小球开始运动所在高度h为$\frac{ssinθ}{2}$,时间最短,最短时间为$2\sqrt{\frac{s}{gsinθ}}$.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,本题对数学能力的要求较高,需加强这方面的训练.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 一只小灯泡,标有“3V、0.6W”字样.现用下面给出的器材测量该小灯泡正常发光时的电阻R1.(滑动变阻器最大阻值为10Ω;电源电动势为12V,内阻约为1Ω;电流表内阻约为1Ω,电压表的内阻约为10kΩ).
一只小灯泡,标有“3V、0.6W”字样.现用下面给出的器材测量该小灯泡正常发光时的电阻R1.(滑动变阻器最大阻值为10Ω;电源电动势为12V,内阻约为1Ω;电流表内阻约为1Ω,电压表的内阻约为10kΩ).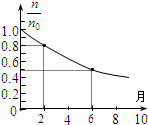 如图所示为某种放射性元素的衰变规律(纵坐标$\frac{n}{{n}_{0}}$表示任意时刻放射性元素的原子数与t=0时的原子数之比),则该放射性元素的半衰期是180天(一个月按30天计算).在从某古迹中发掘出来的木材中,所含${\;}_{6}^{14}$C的比例是正在生长的植物中的80%,放射性${\;}_{6}^{14}$C的半衰期是5700年,根据图象可以推算,该古迹距今约1900年.
如图所示为某种放射性元素的衰变规律(纵坐标$\frac{n}{{n}_{0}}$表示任意时刻放射性元素的原子数与t=0时的原子数之比),则该放射性元素的半衰期是180天(一个月按30天计算).在从某古迹中发掘出来的木材中,所含${\;}_{6}^{14}$C的比例是正在生长的植物中的80%,放射性${\;}_{6}^{14}$C的半衰期是5700年,根据图象可以推算,该古迹距今约1900年.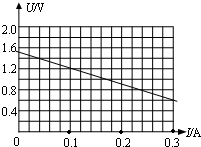 如图所示,用测电源电动势和内阻的实验中,通过改变滑动变阻器,得到U-I图线;测得电动势E=1.5V,内阻r=3Ω.
如图所示,用测电源电动势和内阻的实验中,通过改变滑动变阻器,得到U-I图线;测得电动势E=1.5V,内阻r=3Ω.