Question

【题目】运动员沿竖直方向做跳伞训练，打开降落伞后的速度时间图象如图a所示。降落伞用8根对称的绳悬挂运动员，每根绳与中轴线的夹角均为37°，如图b所示。已知运动员的质量为64kg，降落伞的质量为16kg，假设打开伞后伞所受阻力f的大小与速率v成正比，即f=kv。取g=10m/s2，sin37°=0.6，cos37°=0.8，则

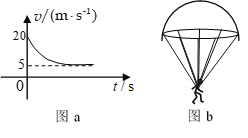
A.k=200N·s/m

B.打开伞后瞬间运动员的加速度方向竖直向上

C.打开伞后瞬间运动员的加速度大小为20m/s2

D.每根悬绳能够承受的拉力至少为400N

Answer 1

【答案】BD

【解析】

A.由速度时间图像可知，当速度为时，运动员匀速运动，故

解得，故A错误；

B. 打开伞后瞬间运动员做减速运动，故加速度方向竖直向上，B正确；

C. 打开伞后瞬间由牛顿第二定律

解得，故C错误；

D.打开伞的瞬间，加速度最大，绳中拉力最大，对运动员可得

解得，故D正确。

故选BD。