题目内容
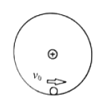
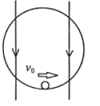
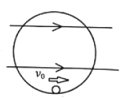
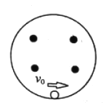
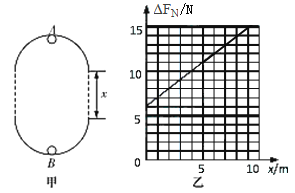
【题目】甲图为某研究小组研究小球对轨道压力的装置原理图。在同一竖直平面内两正对着的相同半圆光滑轨道相隔一定的距离x，虚线沿竖直方向，一小球能在其间运动，为了测试小球对轨道的压力，今在最低点与最高点各放一个压力传感器，并通过计算机显示出来，当轨道距离x变化时，记录两点压力差ΔFN与距离x的数据、作出ΔFN－x图象如乙图所示。(不计空气阻力，g取10 m/s2)求：
(1)小球的质量和半圆轨道的半径；
(2)若小球在最低点B的速度为20 m/s，为使小球能始终沿光滑轨道运动，ΔFN的最大值。
【答案】(1)0.1kg，2m (2)21N
【解析】试题分析：小球在运动过程中，机械能守恒，分别对小球在AB两点时进行受力分析，结合图象列出在这两点的压力差的关系式，结合图象中的截距，可得知小球的质量，从而可计算出轨道的半径。从B到A，由机械能守恒定律求出小球到达A点的速度，在A点，由牛顿第二定律、第三定律结合求得ΔFN的最大值。
(1)设轨道半径为R，由机械能守恒定律：
①
在B点：
②
在A点：
③
由①②③式得：两点的压力差
④
由图象得：截距6mg=6 N，得m=0.1 kg⑤
由④式可知：因为图线的斜率
所以R=2 m⑥
(2)在A点不脱离轨道的条件为：
⑦
由①⑥⑦三式和题中所给已知条件解得：x≤15 m⑧
代入④得：
练习册系列答案
教材全解字词句篇系列答案
相关题目
