题目内容
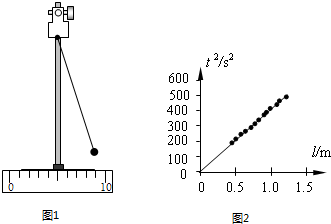 (2009?上海模拟)某同学利用如图1所示的装置测量当地的重力加速度.实验步骤如下:
(2009?上海模拟)某同学利用如图1所示的装置测量当地的重力加速度.实验步骤如下:A.按装置图安装好实验装置;
B.用三角尺测量小球的直径 d;
C.用米尺测量悬线的长度 l;
D.让小球在竖直平面内小角度摆动.当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3….当数到20时,停止计时,测得时间为 t;
E.多次改变悬线长度,对应每个悬线长度,都重复实验步骤C、D;
F.计算出每个悬线长度对应的 t2;
G.以 t2 为纵坐标、l 为横坐标,作出 t2-l 图象.
(1)该同学根据实验数据,利用计算机作出 t2-l图象如图2所示.根据图象拟合得到方程为:t2=404.0l+3.5(s2).由此可以得出当地的重力加速度g=
9.76
9.76
m/s2.(取π2=9.86,结果保留3位有效数字)(2)图象没有过坐标原点的原因可能是
D
D
(A) 不应在小球经过最低点时开始计时,应该在小球运动到最高点开始计时
(B) 开始计时后,不应记录小球经过最低点的次数,而应记录小球全振动的次数
(C) 不应作 t2-l 图象,而应作 t-l 图象
(D) 不应作 t2-l 图象,而应作 t2-(l+
| 1 | 2 |
分析:(1)根据单摆周期公式求出t2-l函数关系式,然后求出重力加速度.
(2)单摆摆长等于摆线长度与摆球半径之和,以摆线长度作为摆长,则摆长偏小.
(2)单摆摆长等于摆线长度与摆球半径之和,以摆线长度作为摆长,则摆长偏小.
解答:解:(1)由题意知,单摆的周期T=
=
由单摆周期公式T=2π
可得:t2=
l
由图象得到的方程为:t2=404.0l+3.5,
则
=404.0,
g=
≈9.76m/s2;
③单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,
摆长小于实际摆长,t2-l图象不过原点,在纵轴上截距不为零,故D正确,故选D;
故答案为:9.76; D
| t | ||
|
| t |
| 10 |
由单摆周期公式T=2π
|
可得:t2=
| 400π2 |
| g |
由图象得到的方程为:t2=404.0l+3.5,
则
| 400π2 |
| g |
g=
| 400π2 |
| 404 |
③单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,
摆长小于实际摆长,t2-l图象不过原点,在纵轴上截距不为零,故D正确,故选D;
故答案为:9.76; D
点评:理解用单摆测定重力加速度的原理及实验方法、数据处理,难度不大,属于基础题.

练习册系列答案
相关题目
 (2009?上海模拟)如图所示,质量为M=2kg的长木板上表面光滑,与水平地面的动摩擦因数为μ=0.2,在板上放有两个小物块,可看作质点,左边的小物块质量为 m1=1.5kg,距木板左端x1=8m,右边的小物块质量为m2=0.5kg,与m1的距离为x2=4m.现敲击木板左端使其瞬间获得10m/s向右的初速度.求:
(2009?上海模拟)如图所示,质量为M=2kg的长木板上表面光滑,与水平地面的动摩擦因数为μ=0.2,在板上放有两个小物块,可看作质点,左边的小物块质量为 m1=1.5kg,距木板左端x1=8m,右边的小物块质量为m2=0.5kg,与m1的距离为x2=4m.现敲击木板左端使其瞬间获得10m/s向右的初速度.求: (2009?上海模拟)如图所示,在一只烧瓶口插入一细玻璃管,管的另一端与一水银压强计相通,烧瓶中封闭着一定质量的理想气体,开始时气压计的U形管的两水银面一样高.现将瓶浸入热水中,改变烧瓶中气体的温度,则下面操作中正确的是( )
(2009?上海模拟)如图所示,在一只烧瓶口插入一细玻璃管,管的另一端与一水银压强计相通,烧瓶中封闭着一定质量的理想气体,开始时气压计的U形管的两水银面一样高.现将瓶浸入热水中,改变烧瓶中气体的温度,则下面操作中正确的是( ) (2009?上海模拟)一质点自x轴原点O出发,沿正方向以加速度a运动,经过to时间速度变为v0,接着以-a加速度运动,当速度变为-
(2009?上海模拟)一质点自x轴原点O出发,沿正方向以加速度a运动,经过to时间速度变为v0,接着以-a加速度运动,当速度变为- (2009?上海模拟)如图所示,铜棒ab长0.1m,质量为0.06kg,两端与长为0.15m的轻铜线相连,静止于竖直平面上,整个装置处在竖直向下的匀强磁场中,磁感应强度为B=0.5T,现接通电源,使铜棒中保持有恒定电流通过,铜棒发生摆动.已知最大偏转角为37°,则在摆到最大偏角的过程中铜棒的重力势能增加了
(2009?上海模拟)如图所示,铜棒ab长0.1m,质量为0.06kg,两端与长为0.15m的轻铜线相连,静止于竖直平面上,整个装置处在竖直向下的匀强磁场中,磁感应强度为B=0.5T,现接通电源,使铜棒中保持有恒定电流通过,铜棒发生摆动.已知最大偏转角为37°,则在摆到最大偏角的过程中铜棒的重力势能增加了