题目内容
6. 如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )| A. | 168cm | B. | 56cm | C. | 42cm | D. | 30cm | ||||
| E. | 24cm |
分析 根据a、b两点状态状态,结合波形,确定ab间距离与波长的关系,求出波长的通项,再得到波长的特殊值.
解答 解: 题中给出,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,若该波向右传播,如图所示,则ab间距离为$\frac{3}{4}$λ或1$\frac{3}{4}$λ或2$\frac{3}{4}$λ…,得到通式xab=(k+$\frac{3}{4}$)λ(k=0,1,2…),由此可得到波长的可能值
题中给出,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,若该波向右传播,如图所示,则ab间距离为$\frac{3}{4}$λ或1$\frac{3}{4}$λ或2$\frac{3}{4}$λ…,得到通式xab=(k+$\frac{3}{4}$)λ(k=0,1,2…),由此可得到波长的可能值
λ=$\frac{{x}_{ab}}{k+\frac{3}{4}}$=$\frac{168}{4k+3}$cm
当k=0时,得到λ=56cm,此为波长最大值.
当k=1时,λ=24cm,
若改变向左传播,则ab间距离为$\frac{1}{4}$λ或1$\frac{1}{4}$λ或2$\frac{1}{4}$λ…,得到通式xab=(k+$\frac{1}{4}$)λ(k=0,1,2…),由此可得到波长的可能值
λ=$\frac{{x}_{ab}}{k+\frac{1}{4}}$=$\frac{168}{4k+1}$cm
当k=0时,得到λ=168cm,此为波长最大值.
当k=1时,λ=33.6cm,
故选:ABE
点评 本题知道两个质点的状态,通过画出波形,确定出两点距离与波长的关系是常用的思路.要注意波传播的方向可能向左,也可能向右.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.下列说法正确的是( )
| A. | 布朗运动反映了液体分子的无规则运动 | |
| B. | 给自行车轮胎打气,越来越费力,说明气体分子间斥力在增大 | |
| C. | 放在水面上的硬币可以浮在水面上是因为硬币所受浮力等于重力 | |
| D. | 利用太阳能装置使机械长久运动下去,这并不违背热力学第二定律 |
15.我国已建成的秦山、大亚湾等十几座核电站,有效的解决了工农业生产中的电力需求问题.目前这些正在工作中的核电站利用的是( )
| A. | 放射性元素衰变放出的能量 | B. | 人工放射性同位素衰变放出的能量 | ||
| C. | 重核裂变放出的能量 | D. | 轻核聚变放出的能量 |
16.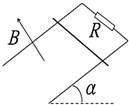 如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )
如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )
 如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )
如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )| A. | 在此过程中流过电阻R的电量为$\frac{Blx}{R+r}$ | |
| B. | 金属杆下滑的最大速度vm=$\frac{mgRsinα}{{B}^{2}{l}^{2}}$ | |
| C. | 在此过程中电阻R产生的焦耳热为mgxsinα-$\frac{1}{2}$mvm2 | |
| D. | 在此过程中导体棒克服安培力做功为$\frac{r}{R+r}$(mgxsinα-$\frac{1}{2}$mvm2) |
 一定质量的理想气体被活塞封闭在竖直放置的绝热气缸内,活塞的质量为1kg,横截面积s=5cm2,活塞可沿气缸壁无摩擦滑动且不漏气.开始活塞距气缸底部10cm,气体温度为27℃,现在对气缸内气体缓缓加热,活塞上升了5cm,已知大气压强p0=1.0×105Pa,g=10m/s2,求:
一定质量的理想气体被活塞封闭在竖直放置的绝热气缸内,活塞的质量为1kg,横截面积s=5cm2,活塞可沿气缸壁无摩擦滑动且不漏气.开始活塞距气缸底部10cm,气体温度为27℃,现在对气缸内气体缓缓加热,活塞上升了5cm,已知大气压强p0=1.0×105Pa,g=10m/s2,求:
 触但不粘连,B点为弹簧自由端,光滑水平面AB与倾角θ=37°的倾斜面BC在B处平滑连接,OCD在同一条竖直线上,CD右端是半径为R=CD=0.4m的$\frac{1}{4}$光滑圆弧,斜面BC与圆弧在C处也平滑连接,物块甲与斜面BC间的动摩擦因数μ=0.3.现用力将物块甲缓慢向左压缩弹簧,使弹簧获得一定能量后撤去外力,物块甲刚好能滑到C点,与此同时用长L=0.9m的细线悬挂于O点的小物块乙从图示位置静止释放,α=60°,物块乙到达C点时细线恰好断开且与物块甲发生正碰,碰撞后物块甲恰好对圆弧轨道无压力,物块乙恰好从图中P点离开圆弧轨道,取g=10m/s2,$\sqrt{10}$=3,求:
触但不粘连,B点为弹簧自由端,光滑水平面AB与倾角θ=37°的倾斜面BC在B处平滑连接,OCD在同一条竖直线上,CD右端是半径为R=CD=0.4m的$\frac{1}{4}$光滑圆弧,斜面BC与圆弧在C处也平滑连接,物块甲与斜面BC间的动摩擦因数μ=0.3.现用力将物块甲缓慢向左压缩弹簧,使弹簧获得一定能量后撤去外力,物块甲刚好能滑到C点,与此同时用长L=0.9m的细线悬挂于O点的小物块乙从图示位置静止释放,α=60°,物块乙到达C点时细线恰好断开且与物块甲发生正碰,碰撞后物块甲恰好对圆弧轨道无压力,物块乙恰好从图中P点离开圆弧轨道,取g=10m/s2,$\sqrt{10}$=3,求: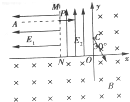 如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求:
如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求: