题目内容
11. 如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求:
如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求:(1)匀强电场的电场强度E2的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)匀强电场的电场强度E1的大小.
分析 (1)研究粒子在电场E2中的类平抛运动,由分速度公式和牛顿第二定律结合求解E2.
(2)画出粒子在磁场中圆周运动的轨迹,由几何关系求出轨迹半径,由洛伦兹力提供向心力,列式求解B.
(3)由几何关系求出AP间的距离,由动能定理求E1.
解答 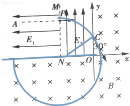 解:(1)粒子在电场E2中作类平抛运动,刚进入磁场时沿y轴负方向的分速度为:vy=v0cot30°=$\sqrt{3}$v0;
解:(1)粒子在电场E2中作类平抛运动,刚进入磁场时沿y轴负方向的分速度为:vy=v0cot30°=$\sqrt{3}$v0;
又 vy=at=$\frac{q{E}_{2}}{m}t$,t=$\frac{L}{{v}_{0}}$
解得:E2=$\frac{\sqrt{3}m{v}_{0}^{2}}{qL}$
(2)粒子进入磁场时的速度大小为:v=$\frac{{v}_{0}}{sin30°}$=2v0;
结合题意,画出轨迹如图.设粒子圆周运动的半径为r,则有:r=$\frac{0.5L}{sin30°}$=L
根据qvB=m$\frac{{v}^{2}}{r}$得:B=$\frac{mv}{qr}$=$\frac{2m{v}_{0}}{qL}$
(3)粒子离开磁场再进入电场后作类平抛运动,沿x轴方向做初速度为零的匀加速直线运动,与粒子从A到P的运动情况相同,由几何关系可知,AP间的距离为:
s=2L-L-L(1-cos30°)=$\frac{\sqrt{3}}{2}$L
粒子从A运动到P时,由动能定理得:
qE1s=$\frac{1}{2}m{v}_{0}^{2}$
联立解得:E1=$\frac{\sqrt{3}m{v}_{0}^{2}}{3qL}$
答:(1)匀强电场的电场强度E2的大小为$\frac{\sqrt{3}m{v}_{0}^{2}}{qL}$;
(2)匀强磁场的磁感应强度B的大小为$\frac{2m{v}_{0}}{qL}$;
(3)匀强电场的电场强度E1的大小为$\frac{\sqrt{3}m{v}_{0}^{2}}{3qL}$.
点评 粒子做类平抛时,由牛顿第二定律与运动学公式相结合来综合运用;在做匀速圆周运动时,由半径公式与几何关系结合处理,同时要抓住各个过程间之间的关系,比如距离关系进行解答.

 阅读快车系列答案
阅读快车系列答案 如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )| A. | 168cm | B. | 56cm | C. | 42cm | D. | 30cm | ||||
| E. | 24cm |
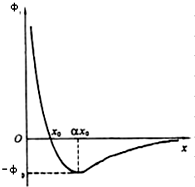 两个点电荷位于x轴上,在它们形成的电场中,若取无限远处的电势为零,则在正x轴上各点的电势如图中曲线所示.电势为零的点的坐标x0,电势为极小值-φ0的点的坐标为ax0(a>2).(已知点电荷的电场中各点的电势φ=k$\frac{Q}{r}$,式中Q为点电荷的电量,r为距点电荷的距离)根据图线提供的信息,以下说法正确的是( )
两个点电荷位于x轴上,在它们形成的电场中,若取无限远处的电势为零,则在正x轴上各点的电势如图中曲线所示.电势为零的点的坐标x0,电势为极小值-φ0的点的坐标为ax0(a>2).(已知点电荷的电场中各点的电势φ=k$\frac{Q}{r}$,式中Q为点电荷的电量,r为距点电荷的距离)根据图线提供的信息,以下说法正确的是( )| A. | 可以确定这两个点电荷必为同种电荷 | |
| B. | 可以求出这两个点电荷的电量大小 | |
| C. | 可以求出这两个点电荷在x轴上的位置坐标 | |
| D. | 可以确定x轴上各点的电场强度均沿+x方向 |
| A. | 这列水波的周期是0.5s | B. | 这列水波的波长为$\frac{5}{3}$m | ||
| C. | 这列水波的速度为1.0m/s | D. | 树叶A在l.Os内沿水面运动1.Om |
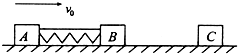 如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=m,mB=mC=2m,A、B用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不栓接).开始时A、B以共同速度v0运动,C静止.某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.求:
如图所示,光滑水平直轨道上有三个滑块A、B、C,质量分别为mA=m,mB=mC=2m,A、B用细绳连接,中间有一压缩的轻弹簧(弹簧与滑块不栓接).开始时A、B以共同速度v0运动,C静止.某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.求: 如图所示,封闭有一定质量理想气体的气缸固定在水平桌面上,开口向右放置,活塞的横截面积为S.活塞通过不可伸长的轻绳连接了一个质量为m=$\frac{{ρ}_{0}S}{2g}$的小物体,轻绳跨在定滑轮上.开始时汽缸内外压强相同,均为大气压p0(为已知).汽缸内气体的温度为T0,轻绳恰好处在伸直状态.不计摩擦,重力加速度为g,现缓慢降低汽缸内温度,求:
如图所示,封闭有一定质量理想气体的气缸固定在水平桌面上,开口向右放置,活塞的横截面积为S.活塞通过不可伸长的轻绳连接了一个质量为m=$\frac{{ρ}_{0}S}{2g}$的小物体,轻绳跨在定滑轮上.开始时汽缸内外压强相同,均为大气压p0(为已知).汽缸内气体的温度为T0,轻绳恰好处在伸直状态.不计摩擦,重力加速度为g,现缓慢降低汽缸内温度,求: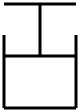 质量为m=2kg的汽缸中有一截面积为S=10cm2的可在汽缸内无摩擦移动的活塞,活塞的质量为M=3kg.一根绳系住活塞,将活塞和汽缸一起吊起,处于平衡状态时活塞与汽缸底相距10cm,大气压强P0=105Pa,取g=10m/s2,当汽缸下面的钩子上挂M1=3kg的重物后,系统重新平衡,求这一过程中汽缸内气体从外界吸收的热量.(设气体温度不变)
质量为m=2kg的汽缸中有一截面积为S=10cm2的可在汽缸内无摩擦移动的活塞,活塞的质量为M=3kg.一根绳系住活塞,将活塞和汽缸一起吊起,处于平衡状态时活塞与汽缸底相距10cm,大气压强P0=105Pa,取g=10m/s2,当汽缸下面的钩子上挂M1=3kg的重物后,系统重新平衡,求这一过程中汽缸内气体从外界吸收的热量.(设气体温度不变) 重庆洋人街有一项惊险刺激的游戏项目高空滑索,游戏者通过绳索悬挂在滑车下,滑车跨在两根钢缆上从高处向下滑去,如图所示.若下滑过程中的某一段可看作人与滑车一起沿钢缆匀速下滑,下滑的速度为15m/s,此段钢缆的倾角为30°,人和滑车的总质量为75kg,空气阻力的大小满足f=kv2,其中v为下滑速度,k为常数,忽略滑车和钢缆间的摩擦,重力加速度取10m/s2,求:
重庆洋人街有一项惊险刺激的游戏项目高空滑索,游戏者通过绳索悬挂在滑车下,滑车跨在两根钢缆上从高处向下滑去,如图所示.若下滑过程中的某一段可看作人与滑车一起沿钢缆匀速下滑,下滑的速度为15m/s,此段钢缆的倾角为30°,人和滑车的总质量为75kg,空气阻力的大小满足f=kv2,其中v为下滑速度,k为常数,忽略滑车和钢缆间的摩擦,重力加速度取10m/s2,求: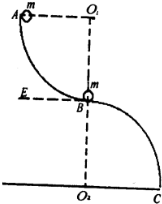 如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)
如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)