题目内容
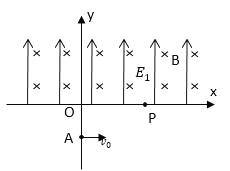
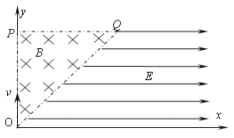
【题目】如图所示，在平面直角坐标系xoy的第一象限内有一边长为L的等腰直角三角形区域OPQ，三角形的O点恰为平面直角坐标系的坐标原点，该区域内有磁感应强度为B、方向垂直于纸面向里的匀强磁场，第一象限中y ≤ L的其它区域内有大小为E、方向沿x轴正方向的匀强电场；一束电子（电荷量为e、质量为m）以大小不同的速度从坐标原点O沿y轴正方向射入匀强磁场区。则：
（1）能够进入电场区域的电子的速度范围；
（2）已知一个电子恰好从P点离开了磁场，求该电子的速度和由O到P的运动时间；
（3）若电子速度为
，且能从x轴穿出电场，求电子穿过x轴的坐标。
【答案】（1）
（2） 
（3）
【解析】
（1）通过Q点进入电场区域的电子速度最大，根据洛伦兹力等于向心力，求出最大速度；
（2）恰好从P点离开了磁场，半径为L/2，画出运动轨迹，根据粒子在磁场中的运动周期和牛顿第二定律，分别求出在磁场和电场中的运动时间，求该电子由O到P的运动时间；
（3）只有当电子第一次从电场返回磁场且不从OP和PQ两边离开磁场时，电子才有可能经电场偏转通过x轴。画出运动轨迹，找出第二次进入电场的位置，根据牛顿第二定律和位移时间关系，求出电子穿过x轴的坐标。
（1）通过Q点进入电场区域的电子速度最大，其半径r1=L
能够进入电场区域的电子的速度范围是0<v≤
（2）设从P点离开磁场的电子半径为r2，轨迹如图所示：
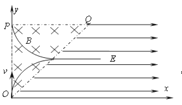
则：r2=L/2
T=
， t1=t3=T/4=
在电场中运动：eE=ma a=
电子由O到P的运动时间：t=t1+t2+t3=
+
（3）只有当电子第一次从电场返回磁场且不从OP和PQ两边离开磁场时，电子才有可能经电场偏转通过x轴，即电子第一次返回磁场时的半径r3满足：r3≤L/3
设电子从O点射入磁场时的速度为v3，轨迹如图所示：
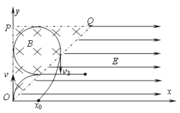
则：
第二次进入电场时的坐标：x=2r3 y=2r3
电子经电场偏转到达x轴的时间：
到达x轴时沿x轴负方向的位移：
坐标为：x=2r3-x0=
