��Ŀ����
����Ŀ����ͼ��ʾ�����ʹ���ˮƽ��֮��ļн�Ϊ30��������A��B�����ľ���Ϊ5m�����ʹ��ڵ綯���Ĵ�������v=2m/s���ٶ������˶����ֽ�һ����Ϊm=10kg��С���壨����Ϊ�ʵ㣩����ڴ��ʹ��ϵ�A�㣬��֪С�����봫�ʹ���Ķ�Ħ������![]() �����ڴ��ʹ���С�����A�㴫�͵�B��Ĺ����У�gȡ10m/s2������
�����ڴ��ʹ���С�����A�㴫�͵�B��Ĺ����У�gȡ10m/s2������
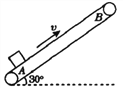
(1)���ʹ���С�������˶��ٹ���
(2)����С����Ĺ����У�ϵͳ������������
���𰸡�(1)W=270J (2) Q= 60J
�����������������������������������������������������ļ��ٶȣ����ȼ���ֱ���˶��ij��ٶȡ�ĩ�ٶȺͼ��ٶ��������λ�ƣ��ж������˶���������ɹ��ܹ�ϵ֪���ʹ���С�������Ĺ�����С�����е�ܵ�������С�����봫�ʹ���Ħ����������������������Ħ��������С�����봫�ʹ�������λ�ƣ����˶�ѧ��ʽ������λ�ƣ�
(1)��С���壺��Ϊ��mgcos����mgsin��������һ��ʼС�������ش��ʹ��������ȼ���ֱ���˶���
��С�������������������ţ�ٵڶ������У���mgcos�ȩ�mgsin��=ma
�������ݽ�ã�a=2.5m/s2
�ɹ�ʽv2=2ax����ȼ����˶���λ��Ϊ�� ![]()
���������봫�ʹ����ٺ�����������
���ݹ��ܹ�ϵ�����ʹ���С�������Ĺ�����С�����е�ܵ���������Ϊ��
![]()
��2��С�����ڼ��ٽ����ȼ����˶������˶�ʱ��Ϊt����С�����˶���λ��Ϊ��
![]()
�����ʱ���ڴ��ʹ��˶���λ��Ϊ��S2=vt
��ã�S2=1.6m
����Ħ����������������Ħ������������������Ծ��룬����
![]()

 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�