题目内容
【题目】如图所示，足够长的长木板AB质量M＝2 kg在水平地面上，可视为质点的木块质量m＝1 kg在长木板的左端A处，木块与长木板保持相对静止一起向右运动，当右端B经过地面上O点时速度为v0＝5 m/s，长木板与P点处的挡板瞬间碰撞后立即以原速率反向弹回，而木块在此瞬间速度不变。已知O点与P点间距离x0＝4.5m，木板与地面间动摩擦因数μ1＝0.1，木块与长木板间动摩擦因数μ2＝0.4，g取10 m/s2。
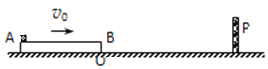
（1）求长木板碰挡板时的速度v1的大小；
（2）当木块与挡板的距离最小时，木块与长木板左端A之间的距离。
【答案】（1）4 m/s（2）4.25 m
【解析】
（1）对木板和木块组成的系统运用牛顿第二定律，求出整体的加速度，结合匀变速直线运动的速度位移公式求出木板碰挡板时的速度大小。
（2）分别对m和M分析，根据牛顿第二定律求出m和M的加速度，结合m和M的运动规律，当木块速度为零时木块与挡板的距离最小，结合运动学公式求出当木块与挡板的距离最小时，木块与长木板左端A之间的距离。
（1）设木块与长木板一起向右运动运动过程中加速度大小为a，则
μ1(m＋M)g＝(m＋M)a
解得 a=1 m/s2。
v1＝4 m/s
（2）设碰撞后木块在长木板上滑动过程中长木板加速度大小为a1，木块加速度大小为a2，则
μ1(m＋M)g +μ2mg=Ma1
μ2mg＝ma2
解得 a1=3.5m/s2，a2＝4m/s2
当木块速度为零时木块与挡板的距离最小，设从与挡板碰撞到木块速度为零经过的时间为t1，长木板通过的距离为x1，木块通过的距离为x2，木块与长木板左端A之间的距离为x3，则
v1＝a2t1
解得 t1＝1 s，x1=2.25 m，x2＝2 m。
x3＝4.25 m
练习册系列答案
相关题目
