题目内容
15．
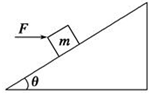如图所示，质量m=1kg的小物块放在倾角为θ=37°的斜面上，物块跟斜面间的动摩擦因数μ=0.2，现用大小为F=20N的水平推力作用于物块，则其上滑加速度为多大？（g取10N/kg，sin 37°=0.6，cos 37°=0.8）
分析 对物体受力分析，抓住垂直斜面方向合力为零，合力沿斜面方向，结合牛顿第二定律求出物块上滑的加速度大小．
解答 解：物块的受力如图所示，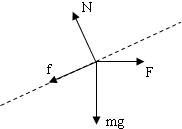
垂直斜面方向合力为零，有：N=mgcos37°+Fsin37°，
沿斜面方向上有：Fcos37°-mgsin37°-f=ma，
f=μN，
联立解得a=$\frac{Fcos37°-mgsin37°-μ（mgcos37°+Fsin37°）}{m}$=$\frac{20×0.8-10×0.6-0.2×（10×0.8+20×0.6）}{1}$=6m/s2．
答：上滑加速度为6m/s2．
点评 解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解，基础题，掌握正交分解的运用．
练习册系列答案
考前必练系列答案
相关题目
10．
如图所示为某磁谱仪部分构件的示意图，永磁铁提供匀强磁场，硅微条径迹探测器可以探测粒子在其中运动的轨迹．宇宙射线中有大量的电子、正电子和质子，当这些粒子从上部垂直进入磁场时，下列说法正确的是（ ）
如图所示为某磁谱仪部分构件的示意图，永磁铁提供匀强磁场，硅微条径迹探测器可以探测粒子在其中运动的轨迹．宇宙射线中有大量的电子、正电子和质子，当这些粒子从上部垂直进入磁场时，下列说法正确的是（ ）| A． | 电子与正电子的偏转方向可能相同 | |
| B． | 电子与正电子在磁场中运动轨迹的半径一定相同 | |
| C． | 仅依据粒子运动轨迹无法判断该粒子是质子还是正电子 | |
| D． | 粒子的动能越大，它在磁场中运动轨迹的半径越小 |
如图所示，在粗糙水平面上相距L=1.0m处，固定有两个绝缘挡板M，N，在它们正中间有一个质量为m=5.0×10-2kg，电荷量为q=-2.0×10-4C的带电物体A（可视为质点），A与水平面间的动摩擦因数μ=0.10，空间有水平向右的匀强电场，场强E=2.5×102V/m．取g=10m/s2，现给A一个初速度v0=3.0m/s向右运动，设A与挡板M，N碰撞过程没有动能损失．求：
3．
一斜面体固定在水平面上，斜面的倾角为θ，物体的质量为m，如图甲所示，在沿斜面向上的力F作用下，物体沿斜面向上做匀速运动；如图乙所示，在沿斜面向下的力$\frac{F}{9}$作用下，物体沿斜面向下做匀速运动，则物体与斜面间的动摩擦因数为（ ）
一斜面体固定在水平面上，斜面的倾角为θ，物体的质量为m，如图甲所示，在沿斜面向上的力F作用下，物体沿斜面向上做匀速运动；如图乙所示，在沿斜面向下的力$\frac{F}{9}$作用下，物体沿斜面向下做匀速运动，则物体与斜面间的动摩擦因数为（ ）| A． | $\frac{5}{4}$cotθ | B． | $\frac{4}{5}$cotθ | C． | $\frac{5}{4}$tanθ | D． | $\frac{4}{5}$tanθ |
火箭内的实验平台有质量为18㎏的测试仪器，火箭从地面起动后以加速度a=$\frac{g}{2}$竖直匀加速上升，g=10m/s2试求：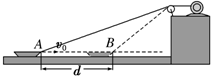
如图，用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边．已知拖动缆绳的电动机功率恒为P，小船的质量为m，小船受到的阻力大小恒为f，经过A点时的速度大小为v0，小船从A点沿直线加速运动到B点经历时间为t1，A、B两点间距离为d，缆绳质量忽略不计．求：
如图所示，有一光滑斜面，斜面的长度为8m，在斜面底端A处有一质量为1kg的小物体，正在以沿斜面向上的初速度v0=10m/s开始向上滑动，已知物体沿斜面滑动时具有沿斜面向下的大小为5m/s2的加速度，求物体到达离顶端0.5m的B处要经过多长时间？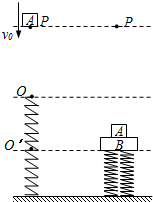
如图所示，轻弹簧一端固定在水平地面上，另一端点在O位置．质量为m=2kg的物块A（可视为质点）以初速度v0=$\sqrt{10}$m/s从弹簧正上方P点向下运动，与弹簧接触后压缩弹簧，将弹簧上端压到O′点位置后，A又被弹簧弹回．物块A离开弹簧后，恰好回到P点．已知OP的距离为x0=0.8m，整个装置放在某种介质中，整个运动过程中物块受到的介质阻力为物块重力的0.25倍，弹簧均在弹性限度内，取g=10m/s2．求：
5．某一质点在几个力作用下处于平衡状态，若使其中一个向西的力逐渐减小，直到为零，其它力保持不变，则在此过程中质点的加速度（ ）
| A． | 方向一定向东，且逐渐减小 | B． | 方向一定向西，且逐渐减小 | ||
| C． | 方向一定向东，且逐渐增大 | D． | 方向一定向西，且逐渐增大 |