题目内容
如图所示,在今年索锲冬奥会冰壶比赛中,某次运动员从投掷线MN放手投掷后,发现冰壶投掷的初速度v0较小,直接滑行不能使冰壶沿虚线到达更近圆心O的位置,于是运动员再冰壶到达前用毛刷摩擦冰壶运行前方的冰面,这样可以使冰壶与冰面间的动摩擦因数从μ减少至某一较小值μ′,恰使冰壶滑行到圆心O点.在运动过程中,以下说法正确的是( )


| A、只要投掷成功,在冰壶直线滑行路径上靠近O点的区间擦冰,擦冰距离要小一些 | B、只要投掷成功,在冰壶直线滑行路径上任意区间擦冰,擦冰距离都是一样的 | C、只要投掷成功,在冰壶直线滑行路径上靠近O点的区间擦冰,冰壶滑行的总时间要小些 | D、只要投掷成功,在冰壶直线滑行路径上任意区间擦冰,冰壶滑行的总时间都一定 |
考点:匀变速直线运动的位移与时间的关系,匀变速直线运动的速度与时间的关系
专题:直线运动规律专题
分析:从发球到O点应用动能定理列出等式找出在冰壶滑行路线上擦冰的距离来进行判断;擦冰区间越靠近投掷线,则开始阶段冰壶的平均速度就越大,总的平均速度越大,距离一定,所以时间越短.
解答:解:A、从发球到O点应用动能定理列出等式可知:-μmgL1-μ′mgL2=0-
m
,所以可以在冰壶滑行路线上的不同区间上擦冰,只要保证擦冰的距离一定就行,A错误,B正确.
C、擦冰区间越靠近投掷线,则开始阶段冰壶的平均速度就越大,总的平均速度越大,距离一定,所以时间越短,故C、D均错误.
故选:B.
| 1 |
| 2 |
| v | 2 0 |
C、擦冰区间越靠近投掷线,则开始阶段冰壶的平均速度就越大,总的平均速度越大,距离一定,所以时间越短,故C、D均错误.
故选:B.
点评:本题关键要分析冰壶的运动情况,能运用动能定理找出擦冰的距离,对于一定距离,先以较大速度运动,再以较小速度运动,总的时间较小.掌握规律是解决问题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
如图为打点计时器打出的纸带,纸带上的点记录了小车运动的信息,下列正确的是( )


| A、小车做加速运动 | B、小车做匀速运动 | C、小车做减速运动 | D、小车在A 点的速度大于在C点的速度 |
一质点做匀加速直线运动,初速度未知,物理课外实验小组的同学们用固定在地面上的频闪照相机对该运动进行研究.已知相邻的两次闪光的时间间隔为1s,发现质点在第1次到第2次闪光的时间间隔内移动了2m,在第3次到第4次闪光的时间间隔内移动了8m,则仅仅由此信息还是不能推算出( )
| A、第1次闪光时质点速度的大小 | B、质点运动的加速度 | C、第2次到第3次闪光时间间隔内质点的位移大小 | D、质点运动的初速度 |
在推导“匀变速直线运动位移的公式”时,把整个运动过程划分为很多小段,每一小段近似为匀速直线运动,然后把各小段位移相加代表整个过程的位移,物理学中把这种方法称为“微元法”.下面几个实例中应用到这一思想方法的是( )
| A、在计算带电体间的相互作用力时,若电荷量分布对计算影响很小,可将带电体看做点电荷 | B、在探究弹性势能的表达式过程中,把拉伸弹簧的过程分成很多小段,在每小段内认为弹簧的弹力是恒力,然后把每小段做功的代数和相加 | C、在探究牛顿第二定律的过程中,控制物体的质量不变,研究物体的加速度与力的关系 | D、在求两个力的合力时,如果一个力的作用效果与两个力的作用效果相同,这个力就是那两个力的合力 |
一个物体在一条直线上做匀加速直线运动,先后经过直线上的A、B两点,已知AB间的距离为4m,物体运动的加速度为2m/s2,则物体到达B点的速度大小可能为( )
| A、2m/s | B、3m/s | C、4m/s | D、5m/s |
自由落体的速度v随时间t变化的图象是( )
A、 | B、 | C、 | D、 |
下列关于直线运动的说法是对的是( )
| A、匀速直线运动的速度是恒定的 | B、匀变速直线运动的瞬时速度随时间改变 | C、速度随时间不断增加的运动,是匀加速直线运动 | D、速度随时间均匀减小的直线运动,是匀减速直线运动 |
下列说法正确的是( )
| A、做匀速直线运动的物体的加速度一定是零? | B、做匀速直线运动的物体的加速度可能是零? | C、做加速直线运动的物体的加速度是零? | D、做减速直线运动的物体的加速度是零 |
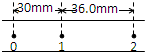 一物体做匀变速运动,某同学通过打点计时器得到了一条较为理想的纸带.他已在每条纸带上按每隔4个点取一个计数点,编号依次为0、1、2、3、4、5.由于不小心纸带被撕断,请根据给出的图中分析纸带的另一部分应该是( )
一物体做匀变速运动,某同学通过打点计时器得到了一条较为理想的纸带.他已在每条纸带上按每隔4个点取一个计数点,编号依次为0、1、2、3、4、5.由于不小心纸带被撕断,请根据给出的图中分析纸带的另一部分应该是( )


