题目内容
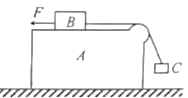
【题目】如图所示,MN是竖直平面内的1/4圆弧轨道,绝缘光滑,半径R=lm。轨道区域存在E = 4N/C、方向水平向右的匀强电场。长L1=5 m的绝缘粗糖水平轨道NP与圆弧轨道相切于N点。质量![]() 、电荷量
、电荷量![]() 的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电,
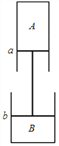
的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电, ![]() ,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间。已知小球a恰能从C板的右端飞出,速度为
,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间。已知小球a恰能从C板的右端飞出,速度为![]() ,小球b打在A板的D孔,D孔距板基端
,小球b打在A板的D孔,D孔距板基端![]() ,A,C板间电势差
,A,C板间电势差![]() ,A,C板间有匀强磁场,磁感应强度5=0.2T,板间距离d=2m,电场和磁编仅存在于两板之间。g=10m/s2求:
,A,C板间有匀强磁场,磁感应强度5=0.2T,板间距离d=2m,电场和磁编仅存在于两板之间。g=10m/s2求:

(1)小球a运动到N点时,轨道对小球的支持力FN多大?
(2 )碰后瞬间,小球a和b的速度分别是多大?
(3 )粗糙绝缘水平面的动摩擦因数![]() 是多大?
是多大?
【答案】(1)![]() (2)
(2)![]() ,
, ![]() (3)
(3)![]()
【解析】试题分析:根据动能定理可求出小球a到达N点时的速度,根据牛顿第二定律可求出小球受到的支持力;的关键通过计算得出小球b做匀速圆周运动.从而求出碰后小球b的速度;根据动量守恒定律可求出碰前瞬间小球a的速度,然后根据动能定理可求出动摩擦因数。
(1)设小球a运动到N点时的速度为vao,则根据动能定理有:
![]()
在N点时根据牛顿第二定律有: ![]()
解得vao = 10m/s FN =11N
(2)设a、b碰撞后电荷量分别是![]() 和
和![]() ,则
,则![]()
设碰后小球a速度为va2,由动能定理有: ![]()
解得:va2= 4m/s
对小球b有: ![]() ,
, ![]()
即mbg = Fb电,所以小球b向上做匀速圆周运动。
设小球b做匀速圆周运动的半径为r,则![]()
设小球b碰后速度为vb2,则![]()
解得:r = 4m vb2=8m/s
(3)设碰撞前,小球a的速度设为va1,由动量守恒定律有
![]()
解得:va1= 8"m/s
小球a从N至P过程中,由动能定理有: ![]()
解得:μ =0.36

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案