Question

【题目】如图甲所示，水平地面上固定一足够长的光滑斜面，斜面顶端有一理想定滑轮，一轻绳跨过滑轮，绳两端分别连接小物块A和B.保持A的质量不变，改变B的质量m.当B的质量连续改变时，得到A的加速度a随B的质量m变化的图线，如图乙所示．设加速度沿斜面向上的方向为正方向，空气阻力不计，重力加速度g取9.8 m/s2，斜面的倾角为θ，下列说法正确的是(　　)

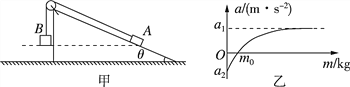
A. 若θ已知，可求出A的质量

B. 若θ未知，可求出乙图中a1的值

C. 若θ已知，可求出乙图中a2的值

D. 若θ已知，可求出乙图中m0的值

Answer 1

【答案】BC

【解析】A、根据牛顿第二定律得：对B得：mg-F=ma;对A得：F-mAgsinθ=mAa;联立得；若θ已知，不能求出A的质量mA．故A错误．B、由变形得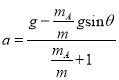．当m→∞时，a=a1=g，故B正确．C、m=0时，a=a2=-gsinθ，故C正确．D、当a=0时，得m=m0=mAsinθ，可知，m0不能求出．故D错误．故选BC.