题目内容
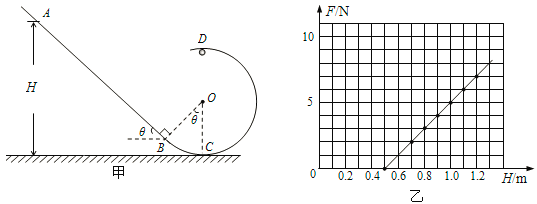
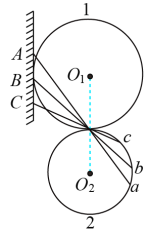
【题目】两个圆1和2外切，它们的圆心在同一竖直线上，有三块光滑的板，它们的一端搭在墙上，另一端搭在圆2的圆周上，三块板都通过两圆的切点，A在圆周上，B在圆内，C在圆外，从ABC三处同时静止释放一个小球，它们都沿光滑板运动，则最先到达圆2的圆周上的球是
A. 从A处释放的球
B. 从B处释放的球
C. 从C处释放的球
D. 同时到达
【答案】B
【解析】设轨道与竖直方向夹角为α，圆的半径为r，则圆内轨道的长度s=2rcosα，下滑的加速度a=
＝gcosα，根据位移时间公式得，x＝
at2，则
即当轨道的端点在圆周上时，沿不同轨道下滑到底端的时间相同；由题意可知．A在圆周上，B在圆内，C在圆外，可知B球下滑的时间最短，即最先到达圆2的圆周上的球是B球，故选B.
练习册系列答案
相关题目
