题目内容
【题目】如图所示，足够长的光滑绝缘水平台左端固定一被压缩的绝缘轻质弹簧，一个质量m=0.04kg、电量
的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能无碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度h=0.45m，倾斜轨道与水平方向夹角为
、倾斜轨道长为L=2.0m，带电小球与倾斜轨道的动摩擦因数
。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强
。（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
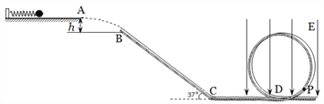
（1）被释放前弹簧的弹性势能
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径应该满足什么条件？
【答案】（1）0.32J（2）
或
【解析】试题分析：释放弹簧后弹簧的弹性势能转化为小球的动能．先根据小球从A到B平抛运动过程，求出小球到B点时竖直分速度，由速度的分解求出到A点的速度，即可根据机械能守恒求解被释放前弹簧的弹性势能；要使小球不离开轨道，有两种情况：第一种情况：是恰好过竖直圆轨道最高点时，先由牛顿第二定律和向心力知识求出到最高点的速度，再由动能定理求解轨道半径．第二种情况：小球恰好到竖直圆轨道最右端，由动能定理求解轨道半径。
（1）小球从A到B平抛运动： 
带入数据解得： 
在B点时速度关系为： 
解得： 
被释放前弹簧的弹性势能： 
（2）在B点时的速度为： 
从B到C根据动能定理得： 
解得： 
好过竖直圆轨道最高点时，根据牛顿第二定律： 
从C到圆轨道最高点： 
因为：qE=0.4N=mg
联立并带入数据解得： 
恰好到竖直圆轨道最右端时： 
带入数据解得： 
要使小球不离开轨道，竖直圆弧轨道的半径
或
。
