题目内容
 如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有根管口比小球略大的竖直细管,管的上口距地面
如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有根管口比小球略大的竖直细管,管的上口距地面| h | 2 |
(1)小球的初速度;
(2)应加电场的场强;
(3)小球落地时的动能.
分析:(1)要使小球无碰撞地通过管口,则当它到达管口时,速度方向为竖直向下,而小球水平方向仅受电场力,做匀减速运动,竖直方向为自由落体运动,可求时间,由分运动的等时性,结合水平方向匀变速运动的位移公式可求水平初速度
(2)已知初速度和位移,由运动学公式可得加速度,结合牛顿第二定律可求电场力和电场强度
(3)对全程应用动能定理求解落地时的动能
(2)已知初速度和位移,由运动学公式可得加速度,结合牛顿第二定律可求电场力和电场强度
(3)对全程应用动能定理求解落地时的动能
解答:解:(1)要使小球无碰撞地通过管口,则当它到达管口时,速度方向为竖直向下,
从抛出到管口过程,竖直方向为自由落体运动,则运动时间t为:
=
gt2
水平方向,粒子做匀减速运动,减速至0
位移:L=
t
解得:v0=2L
(2)水平方向,根据牛顿第二定律:qE=ma
又由运动学公式:02-
=-2as
解得:E=
,方向水平向右
(3)对小球从抛出到落地的全过程应用动能定律:
即:mgh-qEL=EK-
解得:EK=mgh
答:(1)小球的初速度为2L
(2)应加电场的场强为
,方向水平向右
(3)小球落地时的动能为mgh
从抛出到管口过程,竖直方向为自由落体运动,则运动时间t为:
| h |
| 2 |
| 1 |
| 2 |
水平方向,粒子做匀减速运动,减速至0
位移:L=
| v0 |
| 2 |
解得:v0=2L
|
(2)水平方向,根据牛顿第二定律:qE=ma
又由运动学公式:02-
| v | 2 0 |
解得:E=
| 2mgL |
| hq |
(3)对小球从抛出到落地的全过程应用动能定律:
即:mgh-qEL=EK-
| 1 |
| 2 |
| mv | 2 0 |
解得:EK=mgh
答:(1)小球的初速度为2L
|
(2)应加电场的场强为
| 2mgL |
| hq |
(3)小球落地时的动能为mgh
点评:重在建立小球的运动情景,建立运动模型,体会运动过程中遵守的物理规律,注意运用运动的分解的观点解决

练习册系列答案
相关题目
 如图所示,一带电为+q质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰处于静止.若从某时刻起,电场强度减小为原来的1/2,求:(已知sin37°=0.6,cos37°=0.8)
如图所示,一带电为+q质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰处于静止.若从某时刻起,电场强度减小为原来的1/2,求:(已知sin37°=0.6,cos37°=0.8) 如图所示,一带电为+q质量为m的小物快,处于一倾角为37°的光滑绝缘的固定斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰好处于静止.若从某时刻起,只将电场强度大小减小为原来的一半,方向保持不变.求:
如图所示,一带电为+q质量为m的小物快,处于一倾角为37°的光滑绝缘的固定斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰好处于静止.若从某时刻起,只将电场强度大小减小为原来的一半,方向保持不变.求: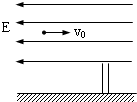 如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有一根管口比小球略大的竖直细管,管的上口距地面
如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有一根管口比小球略大的竖直细管,管的上口距地面