题目内容
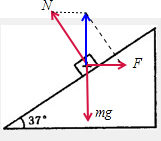
 如图所示,一带电为+q质量为m的小物快,处于一倾角为37°的光滑绝缘的固定斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰好处于静止.若从某时刻起,只将电场强度大小减小为原来的一半,方向保持不变.求:
如图所示,一带电为+q质量为m的小物快,处于一倾角为37°的光滑绝缘的固定斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰好处于静止.若从某时刻起,只将电场强度大小减小为原来的一半,方向保持不变.求:(1)原来电场强度的大小和方向.
(2)场强变化后,物块的加速度大小.
(3)场强变化后,物块下滑距离L时其电势能的变化.
(已知:sin37°=0.6,cos37°=0.8,重力加速度为g)
分析:(1)对小物块进行受力分析,小物块受重力、斜面支持力和电场力三个力作用,电场力水平向右,根据小物块受力平衡列方程可求电场力的大小,在匀强电场中电场力F=qE,在已知F和q的情况下,可以计算出E.
(2)电场强度减小为原来的一半,则小物块受到的电场力减小为原来的一半,物块受到的重力不变,支持力方向不变,小物块在垂直于斜面方向所受合力为0,平行于斜面的方向的合力使物块产生加速度.
(3)根据电场力做功求解电势能的变化.
(2)电场强度减小为原来的一半,则小物块受到的电场力减小为原来的一半,物块受到的重力不变,支持力方向不变,小物块在垂直于斜面方向所受合力为0,平行于斜面的方向的合力使物块产生加速度.
(3)根据电场力做功求解电势能的变化.
解答:解:(1)如图所示,小物块受重力、斜面支持力和电场力三个力作用,受力平衡,运用合成法则有:
qE=mgtan37°
则E=
,方向与电场力方向相同:向右.
(2)电场强度大小减小为原来的一半后,正交分解,
根据牛顿第二定律得:mgsin37°-
qEmgcos37°=ma
得:a=0.3g;
(3)电场力做功为:W=-
qEcos37°?L=-0.3mgL
则物块的电势能增加0.3mgL.
答:(1)原来电场强度的大小为
,方向向右.
(2)场强变化后,物块的加速度大小为0.3g.
(3)场强变化后,物块下滑距离L时其电势能增加0.3mgL.

qE=mgtan37°
则E=
| 3mg |
| 4q |
(2)电场强度大小减小为原来的一半后,正交分解,
根据牛顿第二定律得:mgsin37°-
| 1 |
| 2 |
得:a=0.3g;
(3)电场力做功为:W=-
| 1 |
| 2 |
则物块的电势能增加0.3mgL.
答:(1)原来电场强度的大小为
| 3mg |
| 4q |
(2)场强变化后,物块的加速度大小为0.3g.
(3)场强变化后,物块下滑距离L时其电势能增加0.3mgL.
点评:正确受力分析,根据平衡列方程可得电场力F的大小,又因电场力F=qE,根据受力分析,运用牛顿第二定律进行解答即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有根管口比小球略大的竖直细管,管的上口距地面
如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有根管口比小球略大的竖直细管,管的上口距地面 如图所示,一带电为+q质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰处于静止.若从某时刻起,电场强度减小为原来的1/2,求:(已知sin37°=0.6,cos37°=0.8)
如图所示,一带电为+q质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰处于静止.若从某时刻起,电场强度减小为原来的1/2,求:(已知sin37°=0.6,cos37°=0.8)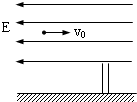 如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有一根管口比小球略大的竖直细管,管的上口距地面
如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有一根管口比小球略大的竖直细管,管的上口距地面