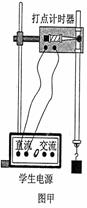
题目内容
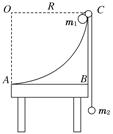
如图所示,位于竖直平面内的1/4 圆弧光滑轨道,半径为R,轨道的最低点B 的切线沿水平方向,轨道上端A 距水平地面高度为H.质量为m 的小球(可视为质点)从轨道最上端A 点由静止释放,经轨道最下端B 点水平飞出,最后落在水平地面上的C 点处,若空气阻力可忽略不计,重力加速度为g.求: 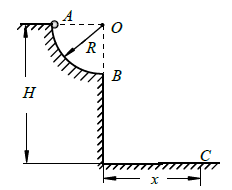
(1)小球运动到B 点时,轨道对它的支持力;
(2)小球落地点C 与B 点的水平距离x;
(3)比值R/H 为多少时,小球落地点C 与B 点水平距离x 最远,及该最大水平距离.
(1)3mg (2)2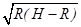 (3)
(3) H(或2R)
H(或2R)
解析试题分析:(1)小球从A点运动到B点的过程中,机械能守恒,设在B点的速度为vB,根据机械能守恒定律有:
mgR=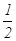 mvB2 (2分)
mvB2 (2分)
设小球在B点时所受轨道的支持力为FN,对小球在B点根据牛顿第二定律有:
FN-mg=m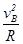 (2分)
(2分)
联立可解得:
FN=3mg (1分)
(2)小球离开B点后做平抛运动:
沿竖直方向有:
H-R=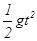 (2分)
(2分)
沿水平方向有:
x=vB t (2分)
联立解得:
x=2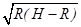 (1分)
(1分)
(3)由x=2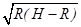 可导出:
可导出:
x=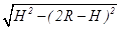
当 时,x有最大值 (1分)
时,x有最大值 (1分)
x的最大值:xm=H(或xm=2R)
考点:圆周运动、平抛运动、机械能守恒

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
关于物体的运动,下列说法中正确的是:
| A.物体在恒力作用下一定做直线运动 |
| B.物体在变力作用下一定做曲线运动 |
| C.物体的速度方向与合外力方向不在同一直线上时,物体做曲线运动 |
| D.加速度不为零且保持不变的运动是匀变速运动 |
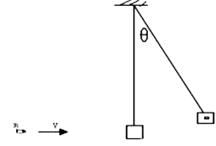
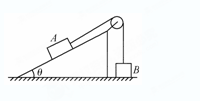
如图所示,套在竖直细杆上的环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大,故在释放B后,A将沿杆上升,当A环上升至定滑轮的连线处于水平位置时,其上升速度v1≠0,若这时B的速度为v2,则
| A.v2=v1 | B.v2>v1 | C.v2≠0 | D.v2=0 |

 。设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度
。设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度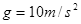 。
。
 点,另一端连接一质量
点,另一端连接一质量 =0.10kg的小球,悬点
=0.10kg的小球,悬点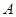 点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到
点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到 点时,轻绳碰到悬点
点时,轻绳碰到悬点