题目内容
10.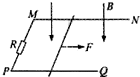 如图所示,两根固定在水平面上的光滑平行金属导轨MN和PQ,一端接有阻值为R的电阻,处于方向竖直向下的匀强磁场中.在导轨上垂直导轨跨放质量为m的金属直杆,金属杆的电阻为r,金属杆与导轨接触良好,导轨足够长且电阻不计.金属杆在垂直于杆的水平恒力F作用下向右匀速运动时,电阻R上的消耗的电功率为P,从某一时刻开始撤去水平恒力F.求撤去水平力后:
如图所示,两根固定在水平面上的光滑平行金属导轨MN和PQ,一端接有阻值为R的电阻,处于方向竖直向下的匀强磁场中.在导轨上垂直导轨跨放质量为m的金属直杆,金属杆的电阻为r,金属杆与导轨接触良好,导轨足够长且电阻不计.金属杆在垂直于杆的水平恒力F作用下向右匀速运动时,电阻R上的消耗的电功率为P,从某一时刻开始撤去水平恒力F.求撤去水平力后:(1)当电阻R上消耗的功率为$\frac{P}{4}$时,金属杆的加速度大小和方向.
(2)求撤去F后直至金属杆静止的整个过程中电阻R上产生的焦耳热.
分析 (1)撤去拉力后,当电阻R上的电功率为$\frac{P}{4}$时,金属杆所受的安培力提供加速度,写出安培力的表达式与牛顿第二定律的表达式即可求加速度.
(2)根据能量守恒定律和能量的分配关系求解电阻R上产生的焦耳热.
解答 解:(1)当金属杆在水平恒力F作用下向右匀速运动时,拉力的功率等于电路中的电功率,即:
Fv=I2(R+r)
据题有 P=I2R
则得:v=$\frac{(R+r)P}{FR}$
由平衡条件有:F=BIL
当电阻R上消耗的功率为$\frac{P}{4}$时,有$\frac{P}{4}$=I′2R,
得:I′=$\frac{I}{2}$
此时:FA′=BI′L=B$\frac{I}{2}$L=$\frac{1}{2}F$
由牛顿第二定律得:FA′=ma
所以:a=$\frac{F}{2m}$,方向水平向左.
(2)撤去F后直至金属杆静止的整个过程中,回路产生的总的焦耳热为:
Q=$\frac{1}{2}m{v}^{2}$=$\frac{m(R+r)^{2}{P}^{2}}{2{F}^{2}{R}^{2}}$
则电阻R上产生的焦耳热为:
QR=$\frac{m(R+r){P}^{2}}{2{F}^{2}R}$
答:(1)当电阻R上消耗的功率为$\frac{P}{4}$时,金属杆的加速度大小是$\frac{F}{2m}$,方向水平向左.
(2)撤去F后直至金属杆静止的整个过程中电阻R上产生的焦耳热是$\frac{m(R+r){P}^{2}}{2{F}^{2}R}$.
点评 本题分析清楚金属杆的运动过程是正确解题的前提与关键;当金属杆受到的安培力与拉力相等时,杆做匀速直线运动,速度达到最大,分别从力和能两个角度进行研究.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.矩形线圈在匀强磁场中转动,产生的交变电动势E=220$\sqrt{2}$sin 100πtV,则这种交流电( )
| A. | 频率是100Hz | B. | 电动势有效值为220V | ||
| C. | 电动势最大值为220V | D. | 周期为0.01秒 |
18.一个物体t=0时刻从坐标原点0由静止开始沿+x方向做匀加速直线运动,速度与坐标的关系为v=$\sqrt{6x}$(m/s),则( )
| A. | 2s末物体的位置坐标x=6m | |
| B. | 2s末物体的位置坐标x=12m | |
| C. | 物体通过区间150m≤x≤600m,所用的时间为20s | |
| D. | 物体通过区间150m≤x≤600m,所用的时间为10s |
15.原子核反应有广泛的应用,如用于核电站等,在下列反应中,属于核裂变反应的是( )
| A. | ${\;}_{5}^{10}$B+${\;}_{0}^{1}$n→${\;}_{3}^{7}$Li+${\;}_{2}^{4}$He | |
| B. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He | |
| C. | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | |
| D. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n |
20.当电阻两端加上某一稳定电压时,通过该电阻的电荷量为0.3C,消耗的电能为1.2J.为在相同时间内使0.6C的电荷量通过该电阻,在其两端需加的电压和消耗的电能分别是( )
| A. | 4V,4.8J | B. | 4V,2.4J | C. | 8V,4.8J | D. | 8V,2.4 |
 如图所示两个同频同向相距8米的振源S1和S2,在介质中传播时的波长为2米,则振动稳定后在S1、S2之间(不包括S1、S2两点)共有7个振动加强的点,有8个点是一直不动的.
如图所示两个同频同向相距8米的振源S1和S2,在介质中传播时的波长为2米,则振动稳定后在S1、S2之间(不包括S1、S2两点)共有7个振动加强的点,有8个点是一直不动的. 如图所示,磁场的方向垂直于xy平面向里.磁感强度B沿y方向没有变化,沿x方向均匀增加,每经过1cm增加量为1.0×10-4T,即△B/△x=1.0×10-4T/cm.有一个长L=20cm,宽h=10cm的不变形的矩形金属线圈,其电阻为0.02Ω,当线圈以v=20cm/s的速度沿x方向运动.问:
如图所示,磁场的方向垂直于xy平面向里.磁感强度B沿y方向没有变化,沿x方向均匀增加,每经过1cm增加量为1.0×10-4T,即△B/△x=1.0×10-4T/cm.有一个长L=20cm,宽h=10cm的不变形的矩形金属线圈,其电阻为0.02Ω,当线圈以v=20cm/s的速度沿x方向运动.问: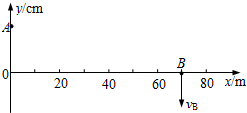 如图所示,A、B是一列沿x轴正方向传播的简谐横波中的两个质点.某时刻质点A正处于y轴上正向最大位移处,另一质点B恰好通过平衡位置向y负方向振动.已知B的横坐标xB=70m,并且该简谐横波的波长λ满足20m<λ<80m.求波长λ.
如图所示,A、B是一列沿x轴正方向传播的简谐横波中的两个质点.某时刻质点A正处于y轴上正向最大位移处,另一质点B恰好通过平衡位置向y负方向振动.已知B的横坐标xB=70m,并且该简谐横波的波长λ满足20m<λ<80m.求波长λ.