题目内容
【题目】过山车是一种惊险的游乐工具,其运动轨道可视为如图所示的物理模型。已知轨道最高点A离地面高为20m,圆环轨道半径为5m,过山车质量为50kg, g=10m/s2,求:
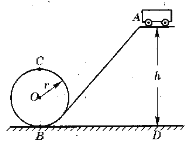
(1)若不计一切阻力,该车从A点静止释放后,经过最低点B时的速度为多大?
(2)当过山车经过圆形轨道最高点C时,轨道对车的作用力为多大?
(3)若考虑阻力的影响,当过山车经过C点时对轨道恰好无压力,则在过山车从A点运动至C点的过程中,克服阻力做的功为多大?
【答案】(1)![]() (2)
(2)![]() (3)3750J
(3)3750J
【解析】
(1)由mgh=![]() mv2
mv2
可知![]() =20m/s;
=20m/s;
(2)A到C的过程中,由机械能守恒可知:mg(h2r)=![]() ,
,
解得![]() ,
,
在C点时由:F+mg=![]()
解答F=1500N.
(3)A到C的过程中,由动能定理可知:mg(h2r)W=![]() (1)
(1)
又因为山车经过C点时对轨道恰好无压力,所以:mg=![]() (2)
(2)
由(1)(2)可知:W=mg(h2r)![]() =3750J,
=3750J,
答:(1)经过最低点B时的速度为20m/s.
(2)当过山车经过圆形轨道最高点C时,轨道对车的作用力为1500N.
(3)过山车从A点运动至C点的过程中,克服阻力做的功为3750J.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目