题目内容
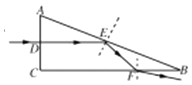
【题目】如图所示,截面为直角三角形ABC的玻璃三棱镜置于空气中,一细光束从D点垂直于AC面入射,AD=CD=a,∠B=30°,棱镜的折射率n= ![]() .求:
.求:
(1)光从棱镜第一次射入空气时的折射角;
(2)光从棱镜第一次射入空气的位置与B点的距离.
【答案】
(1)
解:光在棱镜中的光路如图所示,在AB面上的入射角 i1=60°,设玻璃对空气的临界角为C,则:
sinC= ![]() =
= ![]() ,C=45°,
,C=45°,
由于i1>45°,故光在AB面上发生全反射.
由几何关系知光在CB面上的入射角 i2=30°<C
所以光从棱镜第一次从CB面射入空气.
由折射定律有:n= ![]()
得光从棱镜第一次射入空气时的折射角 r2=45°
(2)
解:由几何知识可知,BE=AE=2a,△BEF为等腰三角形,有:
BF= ![]()
解得光从棱镜第一次射入空气的位置与B点的距离为:BF= ![]() a
a
【解析】(1)画出光路图,由几何知识确定光线射到AB面上的入射角,与临界角C比较,判断能否发生全反射.再运用同样的思路分析光线在BC面上能否发生全反射,若不发生全反射,光线将从棱镜第一次射入空气,由折射定律求解折射角.(2)结合光路图,根据几何知识求光从棱镜第一次射入空气的位置与B点的距离.
【考点精析】掌握光的折射是解答本题的根本,需要知道光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目