题目内容
13.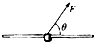 将质量为m的圆环套在固定的水平直杆上,环的直径略大于杆的截面直径,环与杆间动摩擦因数μ,对环施加一位于竖直平面内斜向上,与杆夹角θ的拉力F,使圆环以a的加速度沿杆运动,则F的大小不可能是( )
将质量为m的圆环套在固定的水平直杆上,环的直径略大于杆的截面直径,环与杆间动摩擦因数μ,对环施加一位于竖直平面内斜向上,与杆夹角θ的拉力F,使圆环以a的加速度沿杆运动,则F的大小不可能是( )| A. | $\frac{ma+μmg}{cosθ+μsinθ}$ | B. | $\frac{ma-μmg}{cosθ-μsinθ}$ | ||
| C. | $\frac{ma}{sinθ}$ | D. | $\frac{mg}{sinθ}$ |
分析 对环受力分析,受重力、拉力、弹力和摩擦力,其中弹力可能向上,也可能向下;要分两种情况根据牛顿第二定律列方程求解即可.
解答 解:对环受力分析,受重力、拉力、弹力和摩擦力;其中弹力可能向上,也可能向下,也可能等于0.
1.若环受到的弹力为0,则:Fcosθ=ma;Fsinθ=mg
解得:$F=\frac{mg}{sinθ}$,或$F=\frac{ma}{cosθ}$
2.若环受到的弹力的方向向上,则:
Fcosθ-μ(mg-Fsinθ)=ma
所以:$F=\frac{ma+μmg}{cosθ+μsinθ}$
3.若环受到的弹力的方向向下,则:
Fcosθ-μ(Fsinθ-mg)=ma
所以:F=$\frac{ma-μmg}{cosθ-μsinθ}$
所以ABD是可能的,选项C是不可能的.
本题选择不可能的,故选:C
点评 本题要分三种情况对物体受力分析,然后根据平衡条件和牛顿第二定律列方程求解,关键是分情况讨论.

练习册系列答案
相关题目
4.一物体在地面附近以大小为6m/s2的加速度减速上升过程中( )
| A. | 机械能一定减少 | B. | 机械能一定增加 | ||
| C. | 机械能一定不变 | D. | 无法判断机械能如何变化 |
1.如图1为“探究弹簧弹力与弹簧伸长量关系”的实验装置图,弹簧的上端固定在铁架台上,下端装有指针及挂钩,指针恰好指向一把竖直立起的毫米刻度尺.
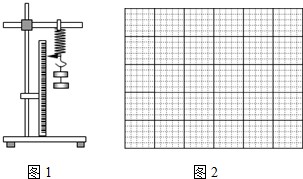
现在测得在挂钩上挂上一定数量钩码时指针在刻度尺上的读数如下表:
已知所有钩码的质量均为m0=50g,当地重力加速度g=9.8m/s2.请回答下列问题:
(1)请根据表格数据在坐标纸中如图2作出n-xn图线,根据图线求出弹簧的劲度系数k=31N/m.(结果保留两位有效数字)
(2)考虑到弹簧自身的重力,上述测量的劲度系数等于(选填“大于”、“小于”或“等于”)真实值.

现在测得在挂钩上挂上一定数量钩码时指针在刻度尺上的读数如下表:
| 钩码数n | 0 | 1 | 2 | 3 | 4 | 5 |
| 刻度尺读数xn/cm | 2.62 | 4.17 | 5.70 | 7.22 | 8.84 | 10.43 |
(1)请根据表格数据在坐标纸中如图2作出n-xn图线,根据图线求出弹簧的劲度系数k=31N/m.(结果保留两位有效数字)
(2)考虑到弹簧自身的重力,上述测量的劲度系数等于(选填“大于”、“小于”或“等于”)真实值.
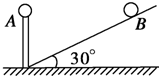 如图所示,A、B是两个带等量同种电荷的小球,A固定在竖直放置的10cm长的绝缘支杆上,B静止于光滑绝缘的倾角为30°的斜面上且恰与A等高,若B的质量为30$\sqrt{3}$g;
如图所示,A、B是两个带等量同种电荷的小球,A固定在竖直放置的10cm长的绝缘支杆上,B静止于光滑绝缘的倾角为30°的斜面上且恰与A等高,若B的质量为30$\sqrt{3}$g;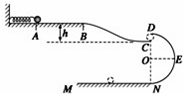 如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求:
如图所示,为一传送装置,其中AB段粗糙,AB段长为L=0.2m,动摩擦因数μ=0.6,BC、DEN段均可视为光滑,且BC的始、末端均水平,具有h=0.1m的高度差,DEN是半径为r=0.4m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过.在左端竖直墙上固定一轻质弹簧,现有一可视为质点的小球,小球质量m=0.2kg,压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿DEN轨道滑下.求: 如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不栓接)置于粗糙水平地面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度为L=0.5m的粗糙水平面,CD与AB相交于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的动摩擦因数均为μ1=0.5,P点为AB上的一个确定点,质量M=0.2kg、可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6)
如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不栓接)置于粗糙水平地面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度为L=0.5m的粗糙水平面,CD与AB相交于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的动摩擦因数均为μ1=0.5,P点为AB上的一个确定点,质量M=0.2kg、可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6) 利用气垫导轨验证机械能守恒定律,实验装置如图所示,水平桌面上固定一倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的小球相连;遮光片两条长边与导轨垂直;导轨上B点有一光电门,可以测量遮光片经过光电门时的挡光时间t,用d表示A点到光电门B处的距离,b表示遮光片的宽度,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度,实验时滑块在A处由静止开始运动
利用气垫导轨验证机械能守恒定律,实验装置如图所示,水平桌面上固定一倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的小球相连;遮光片两条长边与导轨垂直;导轨上B点有一光电门,可以测量遮光片经过光电门时的挡光时间t,用d表示A点到光电门B处的距离,b表示遮光片的宽度,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度,实验时滑块在A处由静止开始运动