题目内容
 (2007?湖南模拟)一质量不计的直角形支架两端分别连接质量均为m的小球A和B.支架的两直角边长度分别为l和2l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
(2007?湖南模拟)一质量不计的直角形支架两端分别连接质量均为m的小球A和B.支架的两直角边长度分别为l和2l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )分析:AB两个球组成的系统机械能守恒,但对于单个的球来说机械能是不守恒的,根据系统的机械能守恒列式可以求得AB之间的关系,同时由于AB是同时转动的,它们的角速度的大小相同.
解答:解:A、OA边转动到处于竖直位置时,A球和B球的速度分别设为vA和vB.
根据题意知两球的角速度相同,线速度之比为vA:vB=ω?2l:ω?2l=2:1;
根据机械能守恒定律得:mg?2l-mgl=
2m
+
m
联立解得,vA=
,故A错误.
B、A球速度最大时,B球的速度也最大,根据系统的机械能守恒可知,两小球的总重力势能最小,故B正确.
C、当OA与竖直方向的夹角为θ时,由机械能守恒得:
mg?2lcosθ-2mg?l(1-sinθ)=
2m
+
m
又vA:vB=2:1;
解得:
=
gl(sinθ+cosθ)-
gl
由数学知识知,当θ=45°时,sinθ+cosθ有最大值,A球速度最大,故C正确;
D、根据动能的表达式Ek=
mv2,vA:vB=2:1;则两球的最大动能之比EEA:EEB=4:1,故D正确.
故选BCD
根据题意知两球的角速度相同,线速度之比为vA:vB=ω?2l:ω?2l=2:1;
根据机械能守恒定律得:mg?2l-mgl=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
联立解得,vA=
2
| ||
| 3 |
B、A球速度最大时,B球的速度也最大,根据系统的机械能守恒可知,两小球的总重力势能最小,故B正确.
C、当OA与竖直方向的夹角为θ时,由机械能守恒得:
mg?2lcosθ-2mg?l(1-sinθ)=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
又vA:vB=2:1;
解得:
| v | 2 A |
| 8 |
| 3 |
| 8 |
| 3 |
由数学知识知,当θ=45°时,sinθ+cosθ有最大值,A球速度最大,故C正确;
D、根据动能的表达式Ek=
| 1 |
| 2 |
故选BCD
点评:本题关键找两个球整体机械能守恒;同时可以根据线速度与角速度的关系公式v=ωr进行分析计算.

练习册系列答案
相关题目
 (2007?湖南模拟)宇航员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点)如图所示,当施加给小球一瞬间水平冲量I时,刚好能使小球在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,万有引力常量为G.
(2007?湖南模拟)宇航员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点)如图所示,当施加给小球一瞬间水平冲量I时,刚好能使小球在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,万有引力常量为G. (2007?湖南模拟)一列简谐波某时刻的波形图如图甲所示,乙图表示该波传播的介质中某质点此后一段时间内的振动图象.则( )
(2007?湖南模拟)一列简谐波某时刻的波形图如图甲所示,乙图表示该波传播的介质中某质点此后一段时间内的振动图象.则( )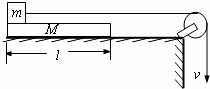 (2007?湖南模拟)如图所示,一块质量为M、长为l的匀质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以恒定的速度υ向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮.求:
(2007?湖南模拟)如图所示,一块质量为M、长为l的匀质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以恒定的速度υ向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮.求: