题目内容
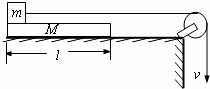 (2007?湖南模拟)如图所示,一块质量为M、长为l的匀质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以恒定的速度υ向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮.求:
(2007?湖南模拟)如图所示,一块质量为M、长为l的匀质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面边缘的定滑轮,某人以恒定的速度υ向下拉绳,物块最多只能到达板的中点,而且此时板的右端尚未到达桌边定滑轮.求:(1)物块与板的动摩擦因数及物块刚到达板的中点时板的位移;
(2)若板与桌面间有摩擦,为使物块能达到板的右端,板与桌面的动摩擦因数的范围;
(3)若板与桌面间的动摩擦因数取(2)问中的最小值,在物块从板的左端运动到右端的过程中,人拉绳的力所做的功(其他阻力均不计)
分析:(1)板与物块都向右做初速度为零的匀加速运动,当两者速度相等时,木块与板相对静止,由牛顿第二定律与运动学公式分析答题.
(2)对板与物块进行受力分析,由牛顿第二定律求出 加速度,由运动学公式求出位移,然后根据两者间位移的几何关系分析答题.
(3)求出物体的位移,然后由功的计算公式求出拉力的功.
(2)对板与物块进行受力分析,由牛顿第二定律求出 加速度,由运动学公式求出位移,然后根据两者间位移的几何关系分析答题.
(3)求出物体的位移,然后由功的计算公式求出拉力的功.
解答:解:(1)设物块在板上滑行的时间为t1,
由 a=
v=at1∴t1=
①
设在此过程中物块前进位移为S1,板前进位移为S2,
则S1=v?t1②S2=
t1③S1-S2=
④
由①②③④得:μ1=
;S2=
;
故物块与板间的摩擦因数为μ1=
,物块到达板的中点时,板的位移S2=
.
(2)设板与桌面间摩擦因数为μ2,物块在板上滑行的时间为t2,
对木板
?t2=v,解得:t2=
,
又设物块从板的左端运动到右端的时间为t3则v?t3-
?t3=l,t3=
,
为了使物块能到达板的右端,必须满足t2≥t3即
≥
μ2≥
,
所以为了使物块能到达板的右端,板与桌面间的摩擦因数μ2≥
;
(3)设绳子的拉力为T,物块从板的左端到达右端的过程中物块的位移为S3,
则有T-μ1mg=0,S3=v?t3=2l,
所以由功的计算公式得:WT=T?S3=μ1mg?2l=
?mg?2l=2Mv2,
所以在物块从板的左端到达板的右端的过程中,绳的拉力做功为2Mv2.
(或W=△EK+△E+W=
Mv2+μ1mgl+μ2(M+m)gl=2Mv2)
答:(1)物块与板的动摩擦因数μ1=
;物块刚到达板的中点时板的位移
;
(2)若板与桌面间有摩擦,为使物块能达到板的右端,板与桌面的动摩擦因数的范围为μ2≥
;
(3)若板与桌面间的动摩擦因数取(2)问中的最小值,在物块从板的左端运动到右端的过程中,人拉绳的力所做的功为2Mv2.
由 a=
| μ1mg |
| M |
| Mv |
| μ1mg |
设在此过程中物块前进位移为S1,板前进位移为S2,
则S1=v?t1②S2=
| v |
| 2 |
| l |
| 2 |
由①②③④得:μ1=
| Mv2 |
| mgl |
| l |
| 2 |
故物块与板间的摩擦因数为μ1=
| Mv2 |
| mgl |
| l |
| 2 |
(2)设板与桌面间摩擦因数为μ2,物块在板上滑行的时间为t2,
对木板
| [μ1mg-μ2(m+M)g] |
| M |
| Mv |
| μ1mg-μ2(m+M)g |
又设物块从板的左端运动到右端的时间为t3则v?t3-
| v |
| 2 |
| 2l |
| v |
为了使物块能到达板的右端,必须满足t2≥t3即
| Mv |
| μ1mg-μ2(m+M)g |
| 2l |
| v |
| Mv2 |
| 2(m+M)gl |
所以为了使物块能到达板的右端,板与桌面间的摩擦因数μ2≥
| Mv2 |
| 2(m+M)gl |
(3)设绳子的拉力为T,物块从板的左端到达右端的过程中物块的位移为S3,
则有T-μ1mg=0,S3=v?t3=2l,
所以由功的计算公式得:WT=T?S3=μ1mg?2l=
| Mv2 |
| mgl |
所以在物块从板的左端到达板的右端的过程中,绳的拉力做功为2Mv2.
(或W=△EK+△E+W=
| 1 |
| 2 |
答:(1)物块与板的动摩擦因数μ1=
| Mv2 |
| mgl |
| l |
| 2 |
(2)若板与桌面间有摩擦,为使物块能达到板的右端,板与桌面的动摩擦因数的范围为μ2≥
| Mv2 |
| 2(m+M)gl |
(3)若板与桌面间的动摩擦因数取(2)问中的最小值,在物块从板的左端运动到右端的过程中,人拉绳的力所做的功为2Mv2.
点评:分析求出物体运动过程、应用牛顿第二定律、运动学公式、功的公式即可正确解题.

练习册系列答案
相关题目
 (2007?湖南模拟)宇航员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点)如图所示,当施加给小球一瞬间水平冲量I时,刚好能使小球在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,万有引力常量为G.
(2007?湖南模拟)宇航员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部最低点静止一质量为m的小球(可视为质点)如图所示,当施加给小球一瞬间水平冲量I时,刚好能使小球在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,月球的半径为R,万有引力常量为G. (2007?湖南模拟)一列简谐波某时刻的波形图如图甲所示,乙图表示该波传播的介质中某质点此后一段时间内的振动图象.则( )
(2007?湖南模拟)一列简谐波某时刻的波形图如图甲所示,乙图表示该波传播的介质中某质点此后一段时间内的振动图象.则( )