题目内容
在某一真空空间内建立xOy坐标系,从原点O处向第I象限发射一荷质比
=104C/kg的带正电的粒子(重力不计).速度大小v0=103 m/s、方向与x轴正方向成30°角.
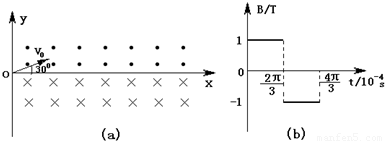
(1)若在坐标系y轴右侧加有匀强磁场区域,在第I、Ⅳ象限,磁场方向垂直xOy平面向外B=1T,求粒子做匀速圆周运动的轨道半径R?
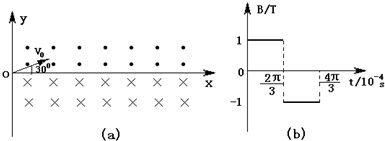
(2)若在坐标系y轴右侧加有匀强磁场区域,在第I象限,磁场方向垂直xOy平面向外;在第Ⅳ象限,磁场方向垂直xOy平面向里;磁感应强度为B=1T,如图(a)所示,求粒子从O点射出后,第2次经过x轴时的坐标x1.
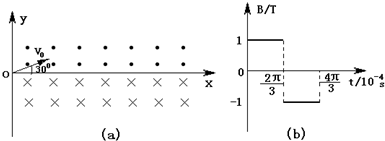
(3)若将上述磁场均改为如图(b)所示的匀强磁场,在t=0到t=
×10-4s时,磁场方向垂直于xOy平面向外;在t=
×10-4s到t=
×10-4s时,磁场方向垂直于xOy平面向里,此后该空间不存在磁场,在t=0时刻,粒子仍从O点以与原来相同的速度v0射入,求粒子从O点射出后第2次经过x轴时的坐标x2.
| q |
| m |

(1)若在坐标系y轴右侧加有匀强磁场区域,在第I、Ⅳ象限,磁场方向垂直xOy平面向外B=1T,求粒子做匀速圆周运动的轨道半径R?
(2)若在坐标系y轴右侧加有匀强磁场区域,在第I象限,磁场方向垂直xOy平面向外;在第Ⅳ象限,磁场方向垂直xOy平面向里;磁感应强度为B=1T,如图(a)所示,求粒子从O点射出后,第2次经过x轴时的坐标x1.
(3)若将上述磁场均改为如图(b)所示的匀强磁场,在t=0到t=
| 2π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
分析:洛伦兹力提供向心力,可以求出粒子运动的半径;根据题目提供的条件,正确画出粒子运动的轨迹,进而确定各点之间的关系.
解答: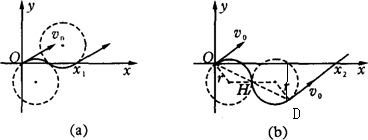 解:(1)设粒子的轨道半径r,洛伦兹力提供向心力,有qvB=m
解:(1)设粒子的轨道半径r,洛伦兹力提供向心力,有qvB=m
,r=0.1m
(2)粒子在x轴上方和下方的磁场中做半径相同的匀速圆周运动,其运动轨迹如图 (a)所示.由几何关系知粒子第二次经过x轴的坐标为x1=2r=0.2 m.
(3)设粒子在磁场中做圆周运动的周期为T.
则T=
=2π×10-4s.
据题意,知粒子在t=0到t=
×10-4s内和在t=
×10-4s到t=
×10-4s时间内在磁场中转过的圆弧所对的圆心角均为
,粒子的运动轨迹应如图 (b)所示.
△ODX2 是低边夹角是30°的等边三角形,
由几何关系得x2=2(2rsin30°+2r)=6r=0.6 m.
答:(1)粒子做匀速圆周运动的轨道半径是0.1m;
(2)第2次经过x轴时的坐标0.2m.
(3)粒子从O点射出后第2次经过x轴时的坐标x2=0.6 m.
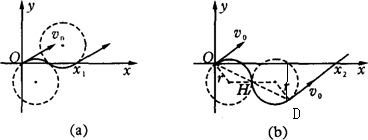 解:(1)设粒子的轨道半径r,洛伦兹力提供向心力,有qvB=m
解:(1)设粒子的轨道半径r,洛伦兹力提供向心力,有qvB=m| v2 |
| r |
(2)粒子在x轴上方和下方的磁场中做半径相同的匀速圆周运动,其运动轨迹如图 (a)所示.由几何关系知粒子第二次经过x轴的坐标为x1=2r=0.2 m.
(3)设粒子在磁场中做圆周运动的周期为T.
则T=
| 2πm |
| Bq |
据题意,知粒子在t=0到t=
| 2π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
| 2π |
| 3 |
△ODX2 是低边夹角是30°的等边三角形,
由几何关系得x2=2(2rsin30°+2r)=6r=0.6 m.
答:(1)粒子做匀速圆周运动的轨道半径是0.1m;
(2)第2次经过x轴时的坐标0.2m.
(3)粒子从O点射出后第2次经过x轴时的坐标x2=0.6 m.
点评:该题考查带电粒子在匀强磁场中的运动,洛伦兹力提供向心力是基础,正确画出粒子运动的轨迹是解决问题的关键.

练习册系列答案
相关题目
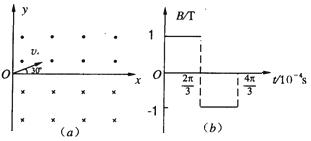
 的带正电的粒子(重力不计),速度大小v=103m/s、方向与x轴正方向成30°角.
的带正电的粒子(重力不计),速度大小v=103m/s、方向与x轴正方向成30°角.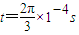 时,磁场方向垂直于xoy平面外;在
时,磁场方向垂直于xoy平面外;在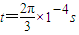 到
到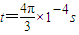 时,磁场方向垂直于xoy平面向里,此后该空间不存在磁场.在t=0时刻,粒子仍从O点以与原来相同的速度v射入,求粒子从O点射出后第2次经过x轴时的坐标x2.
时,磁场方向垂直于xoy平面向里,此后该空间不存在磁场.在t=0时刻,粒子仍从O点以与原来相同的速度v射入,求粒子从O点射出后第2次经过x轴时的坐标x2.