题目内容
在某一真空空间内建立xoy坐标系,从原点O处向第Ⅰ象限发射一比荷 的带正电的粒子(重力不计),速度大小v=103m/s、方向与x轴正方向成30°角.
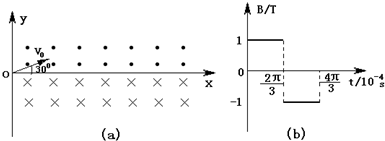
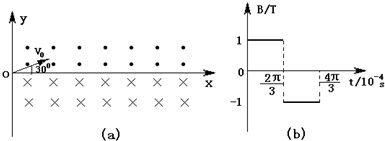
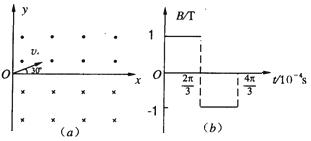
的带正电的粒子(重力不计),速度大小v=103m/s、方向与x轴正方向成30°角.(1)若在坐标系y轴右侧加有匀强磁场区域,在第Ⅰ象限,磁场方向垂直xoy平面向外;在第Ⅳ象限,磁场方向垂直xoy平面向里;磁感应强度均为B=1T,如图(a)所示.求粒子从O点射出后,第2次经过x轴时的坐标x1.
(2)若将上述磁场改为如图(b)所示的匀强磁场.在t=0到
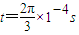 时,磁场方向垂直于xoy平面外;在
时,磁场方向垂直于xoy平面外;在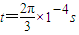 到
到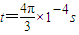 时,磁场方向垂直于xoy平面向里,此后该空间不存在磁场.在t=0时刻,粒子仍从O点以与原来相同的速度v射入,求粒子从O点射出后第2次经过x轴时的坐标x2.
时,磁场方向垂直于xoy平面向里,此后该空间不存在磁场.在t=0时刻,粒子仍从O点以与原来相同的速度v射入,求粒子从O点射出后第2次经过x轴时的坐标x2.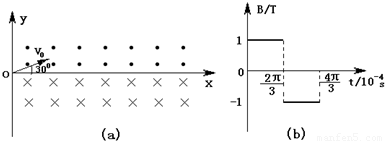
【答案】分析:(1)粒子在磁场中做半径相同的匀速圆周运动,根据牛顿第二定律,由洛伦兹力提供向心力,结合几何关系,即可求解;
(2)根据圆周运动的周期公式,由运动轨迹分时段,从而确定圆弧对应的圆心角,并根据几何关系,从而确定结果.
解答: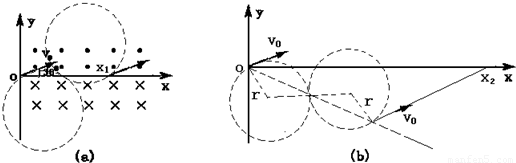 解:(1)粒子在x轴上方和下方的磁场中做半径相同的匀速圆周运动,其运动轨迹如图(a)所示,
解:(1)粒子在x轴上方和下方的磁场中做半径相同的匀速圆周运动,其运动轨迹如图(a)所示,
设粒子的轨道半径r,有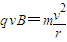 ①
①
代入数据得 r=0.1m ②
由几何关系知x坐标为 x1=2r ③
代入数据得 x1=0.2m ④
(2)设粒子在磁场中的圆周运动的周期为T.
则有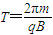 ⑤
⑤
代入数据得:T=2π×10-4s ⑥
根据题意知粒子在t=0到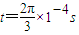 内和
内和
在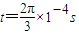 到
到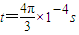 内在磁场中转过圆周弧所对的圆心角均为
内在磁场中转过圆周弧所对的圆心角均为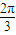 ⑦
⑦
粒子的运动轨迹应如图(b)所示
由几何关系得:x2=6r ⑧
代入数据得:x2=0.6m ⑨
答:(1)粒子从O点射出后,第2次经过x轴时的坐标x1=0.2m.
(2)粒子从O点射出后第2次经过x轴时的坐标x2=0.6m.
点评:考查牛顿第二定律的应用,掌握洛伦兹力公式,理解几何关系在其中的重要性,同时知道圆心角与运动时间的关系.
(2)根据圆周运动的周期公式,由运动轨迹分时段,从而确定圆弧对应的圆心角,并根据几何关系,从而确定结果.
解答:
 解:(1)粒子在x轴上方和下方的磁场中做半径相同的匀速圆周运动,其运动轨迹如图(a)所示,
解:(1)粒子在x轴上方和下方的磁场中做半径相同的匀速圆周运动,其运动轨迹如图(a)所示,设粒子的轨道半径r,有
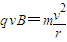 ①
①代入数据得 r=0.1m ②
由几何关系知x坐标为 x1=2r ③
代入数据得 x1=0.2m ④
(2)设粒子在磁场中的圆周运动的周期为T.
则有
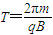 ⑤
⑤代入数据得:T=2π×10-4s ⑥
根据题意知粒子在t=0到
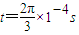 内和
内和在
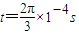 到
到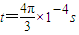 内在磁场中转过圆周弧所对的圆心角均为
内在磁场中转过圆周弧所对的圆心角均为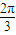 ⑦
⑦粒子的运动轨迹应如图(b)所示
由几何关系得:x2=6r ⑧
代入数据得:x2=0.6m ⑨
答:(1)粒子从O点射出后,第2次经过x轴时的坐标x1=0.2m.
(2)粒子从O点射出后第2次经过x轴时的坐标x2=0.6m.
点评:考查牛顿第二定律的应用,掌握洛伦兹力公式,理解几何关系在其中的重要性,同时知道圆心角与运动时间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目