Question

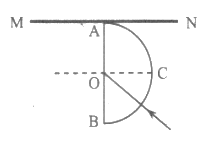
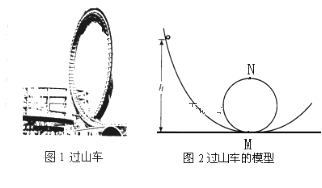
【题目】游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来．我们把这种情况抽象为图2的模型：弧形轨道的下端与竖直圆轨道相接，使小球从弧形轨道上端无初速滚下，小球进入圆轨道下端后沿圆轨道运动，其中M、N分别为圆轨道的最低点和最高点．实验发现，只要h大于一定值，小球就可以顺利通过圆轨道的最高点．如果已知圆轨道的半径为R=5.0m小球质量为m=1.0kg（不考虑摩擦等阻力，）问：

（1）h至少为多大才可使小球沿圆轨道运动而不掉下来．

（2）如果h=15m，小球通过M点时的速度为多大？此时轨道对小球的支持力为多大？

（3）高度h大，小球滑至N点时轨道对小球的压力越大，试推出于h函数关系式．

Answer 1

【答案】(1) 12.5m (2) ，70N (3)

【解析】

(1)小球恰能通过N点即小球通过最高点时恰好不受轨道的压力重力提供向心力即应满足：

小球运动到最高点的过程中只有重力做功，由机械能守恒定律：

联立计算解得：

(2)从开始下落到M点，满足机械能守恒：

计算得出

对M点分析，由牛顿第二定律得：

代入数据计算得出：

(3)小球由静止运动到最高点的过程中机械能守恒则：

小球在最高点在重力和轨道的压力下作圆周运动，对N点分析根据牛顿第二定律得：

计算得出：

答：(1)h至少为时，才可使小球沿圆轨道运动而不掉下来.

(2)如果，小球通过M点时的速度为，此时轨道对小球的支持力为;

(3)于h函数关系式：