题目内容
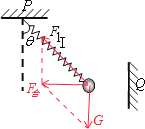
【题目】如图所示,质量为m的球与弹簧I和水平细线II相连,Ⅰ、Ⅱ的另一端分别固定于水平和竖直墙上.弹簧I与竖直方向夹角为θ,球静止时,Ⅰ中的拉力为F1、Ⅱ中的拉力为F2,分析当仅剪断Ⅰ、Ⅱ中的一根的瞬间,下列说法正确的是( )

A. 若剪断Ⅰ,则球的加速度a=g,方向水平向右
B. 若剪断Ⅰ,则球的加速度a=F1/m,方向沿Ⅰ的延长线
C. 若剪断Ⅱ,则球的加速度a=F2/m,方向水平向左
D. 若剪断Ⅱ,则球的加速度a=g,方向竖直向上
【答案】C
【解析】
球原来静止的状态,由平衡条件求出弹簧和细线的拉力.刚剪短细绳时,弹簧来不及形变,故弹簧弹力不能突变;细绳的形变是微小形变,在刚剪短弹簧的瞬间,细绳弹力可突变。根据牛顿第二定律求解瞬间的加速度。
绳子未断时,受力如图,由共点力平衡条件得: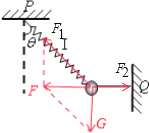
![]() ,
,![]() ,刚剪断弹簧Ⅰ瞬间,细绳弹力突变为零,故小球只受重力,加速度为g,竖直向下,故A B错误;刚剪断细线瞬间,弹簧弹力和重力不变,受力如图:
,刚剪断弹簧Ⅰ瞬间,细绳弹力突变为零,故小球只受重力,加速度为g,竖直向下,故A B错误;刚剪断细线瞬间,弹簧弹力和重力不变,受力如图:
由几何关系,![]() ,因而
,因而![]() ,方向水平向左,故C正确,D错误。所以C正确,ABD错误。
,方向水平向左,故C正确,D错误。所以C正确,ABD错误。

练习册系列答案
相关题目