题目内容
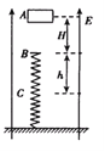
【题目】固定在水平地面上的工件,由AB和BD两部分组成,其中AB部分为光滑的圆弧,∠AOB=37°,圆弧的半径R=0.5m,圆心O点在B点正上方,BD部分水平,长度为![]() =0.2m,C为BD的中点。现有一质量m=1kg的物块(可视为质点),从A端由静止释放,恰好能运动到D点。为使物块运动到C点时速度为零,可先将BD部分以B为轴向上转动一锐角θ,不计物块经过B点时能量损失。sin37°=0.6,cos37°=0.8,g=10m/s2.求:
=0.2m,C为BD的中点。现有一质量m=1kg的物块(可视为质点),从A端由静止释放,恰好能运动到D点。为使物块运动到C点时速度为零,可先将BD部分以B为轴向上转动一锐角θ,不计物块经过B点时能量损失。sin37°=0.6,cos37°=0.8,g=10m/s2.求:
(1)该锐角θ;
(2)物块在BD板上运动的总路程。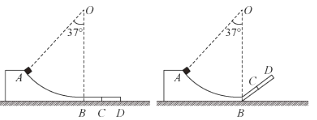
【答案】(1)![]() ; (2)0.25m
; (2)0.25m
【解析】
(1) 设BD段动摩擦因数为![]() ,从A到D的过程,根据动能定理
,从A到D的过程,根据动能定理
![]()
解得
![]()
从A到C的过程中,根据动能定理有
![]()
解得
![]()
(2) 物块在C处速度减为零后,由于![]() 物块将会下滑,而AB段光滑,故物块将做往复运动,直到停止在B点。
物块将会下滑,而AB段光滑,故物块将做往复运动,直到停止在B点。
根据能量守恒定律有
![]()
而摩擦生热为
![]()
代入数据解得物块在BD板上的总路程为
s=0.25m

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目