题目内容
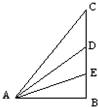如图所示，光滑斜面CA、DA、EA都以AB为底边．三个斜面的倾角分别为75°、45°、30°物体分别沿三个斜面由顶端从静止滑到底端，下面说法中正确的是（ ）| A、物体沿DA滑到底端时具有最大速率 | B、物体沿EA滑到底端所需时间最短 | C、物体沿CA下滑，加速度最大 | D、物体沿CA滑到底端所需时间最短 |
分析：根据动能定理比较物体到达底端时的速度大小．
由物体受力可求出物体下滑的加速度表达式，可知哪个斜面的加速度最大，结合运动学公式求出运行的时间，运用数学三角函数关系求出时间最短的斜面倾角．．
由物体受力可求出物体下滑的加速度表达式，可知哪个斜面的加速度最大，结合运动学公式求出运行的时间，运用数学三角函数关系求出时间最短的斜面倾角．．
解答：解：
A、根据动能定理得：mgh=
mv2，知高度越高，到达底端的速率越大，故物体沿CA滑到底端时具有最大速率，故A错误．
BD、加速度a=gsinθ，设底边长为d，运动的位移：x=
，由
=
at2，解得：t=
=
，可知当θ=45°时，下滑时间最短，故BD错误．
C、加速度a=gsinθ，倾角越大，加速度越大，故C正确．
故选：C
A、根据动能定理得：mgh=
| 1 |
| 2 |
BD、加速度a=gsinθ，设底边长为d，运动的位移：x=
| d |
| cosθ |
| d |
| cosθ |
| 1 |
| 2 |
|
|
C、加速度a=gsinθ，倾角越大，加速度越大，故C正确．
故选：C
点评：解决本题的关键用好动能定理来比较末速度，而不要去用运动学求末速度；其次要利用好几何知识比较时间．
练习册系列答案
相关题目
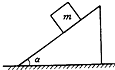如图所示，光滑斜面的倾角为α，一个质量为m物体放在斜面上，如果斜面以加速度a水平向左做匀加速直线运动，物体与斜面相对静止，则斜面对物体的支持力的大小为（ ）
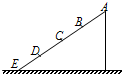如图所示，光滑斜面被等分成四段，AB=BC=CD=DE，一物体从A点静止释放，下列结论正确的是（ ）
如图所示，光滑斜面与水平面在B点平滑连接，质量为0.20kg的物体从斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在水平面上的C点．每隔0.20s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．取g=10m/s2．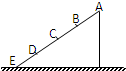
如图所示，光滑斜面被等分成四段，AB=BC=CD=DE，若一物体从A点由静止开始沿斜面向下运动，则（ ）
如图所示，光滑斜面长为a，宽为b，倾角为θ，一小球A沿斜面左上方顶点P水平射入，恰好从下方顶点Q离开斜面，则小球在斜面运动的过程中（ ）| A、加速度的方向始终跟速度方向垂直 | B、加速度的大小始终等于重力加速度 | C、运动规律与平抛运动的规律相同 | D、运动规律与平抛运动的规律不同 |