题目内容
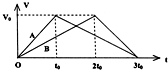 质量均为m的A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )
质量均为m的A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动,撤去F1、F2后受摩擦力的作用减速到停止,其V-t图象如图所示,则下列说法正确的是( )分析:根据速度与时间的图象可知,各段运动的位移关系及之比,同时由牛顿第二定律可得匀减速运动的加速度之比;再由动能定理可得出拉力、摩擦力的关系,及它们的做功关系.
解答:解:由速度与时间图象可知,两个匀减速运动的加速度之比为1:2;由牛顿第二定律可知:A、B受摩擦力大小1:2,故B错误;
由速度与时间图象可知,A、B两物体加速与减速的位移相等,且匀加速运动位移之比1:2,匀减速运动的位移之比2:1,由动能定理可得:A物体的拉力与摩擦力的关系,F1?X-f1?3X=0-0;B物体的拉力与摩擦力的关系,F2?2X-f2?3X=0-0,因此可得:全过程中摩擦力对A、B做功之比1:2;F1、F2对A、B做功之比1:2,F1、F2大小相等.故A正确,B、C错误;
故选AD
由速度与时间图象可知,A、B两物体加速与减速的位移相等,且匀加速运动位移之比1:2,匀减速运动的位移之比2:1,由动能定理可得:A物体的拉力与摩擦力的关系,F1?X-f1?3X=0-0;B物体的拉力与摩擦力的关系,F2?2X-f2?3X=0-0,因此可得:全过程中摩擦力对A、B做功之比1:2;F1、F2对A、B做功之比1:2,F1、F2大小相等.故A正确,B、C错误;
故选AD
点评:解决本题的关键通过图象得出匀加速运动和匀减速运动的加速度,根据牛顿第二定律,得出两个力的大小之比,以及知道速度-时间图线与时间轴所围成的面积表示位移,并运用动能定理.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
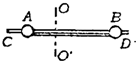 如图所示,质量均为m的A、B两球穿在水平杆C、D上,两球与杆的最大静摩擦力均为fm,OO′为杆CD的转轴.A、B两球之间用一根长为3R的轻绳相连,两球到转轴的距离OA=R,OB=2R.若使杆CD绕OO′轴转动时,A、B两球能保持和杆相对静止,则杆CD转动时角速度的最大值是( )
如图所示,质量均为m的A、B两球穿在水平杆C、D上,两球与杆的最大静摩擦力均为fm,OO′为杆CD的转轴.A、B两球之间用一根长为3R的轻绳相连,两球到转轴的距离OA=R,OB=2R.若使杆CD绕OO′轴转动时,A、B两球能保持和杆相对静止,则杆CD转动时角速度的最大值是( )A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
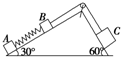 一直角三角块按如图所示放置,质量均为m的A、B两物体用轻质弹簧相连放在倾角为30°的直角边上,物体C放在倾角为60°的直角边上,B与C之间用轻质细线连接,A、C的质量比为
一直角三角块按如图所示放置,质量均为m的A、B两物体用轻质弹簧相连放在倾角为30°的直角边上,物体C放在倾角为60°的直角边上,B与C之间用轻质细线连接,A、C的质量比为
| ||
| 4 |
| A、物体A、B均受到摩擦力作用且等大反向 | ||
B、物体A所受摩擦力大小为
| ||
C、弹簧处于拉伸状态,A、B两物体所受摩擦力大小均为
| ||
| D、剪断弹簧瞬间,物体A一定加速下滑 |
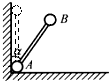 如图所示,质量均为m的A、B两个小球固定在长度为L的轻杆两端,直立在相互垂直的光滑墙壁和地板交界处.突然发生微小的扰动使杆无初速倒下,求当杆与竖直方向成角α时(α<arccos
如图所示,质量均为m的A、B两个小球固定在长度为L的轻杆两端,直立在相互垂直的光滑墙壁和地板交界处.突然发生微小的扰动使杆无初速倒下,求当杆与竖直方向成角α时(α<arccos 如图甲质量均为m的A、B两球间有压缩的轻短弹簧处于锁定状态,放置在水平面上竖直光滑的发射管内(两球紧靠弹簧不相连,两球的大小尺寸和弹簧尺寸都可忽略,它们整体视为质点),解除锁定后,A球能上升的最大高度为H.如图乙现让两球包括锁定的弹簧从水平面出发,沿光滑的半径为R=2H的半圆槽从左侧由静止开始下滑,滑至最低点时,瞬间解除锁定.求:
如图甲质量均为m的A、B两球间有压缩的轻短弹簧处于锁定状态,放置在水平面上竖直光滑的发射管内(两球紧靠弹簧不相连,两球的大小尺寸和弹簧尺寸都可忽略,它们整体视为质点),解除锁定后,A球能上升的最大高度为H.如图乙现让两球包括锁定的弹簧从水平面出发,沿光滑的半径为R=2H的半圆槽从左侧由静止开始下滑,滑至最低点时,瞬间解除锁定.求: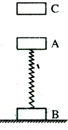 如图所示,质量均为M的A、B两个物块用劲度系数为K的轻弹簧相连,竖直地静置于水平地面.此时弹簧的弹性势能为E0,现将质量也为M的物块C由A的正上方距A物块h高处由静止释放,下落后与A发生碰撞,碰后C与A立即-起向下运动,但C与A不粘连,不计空气阻力.求
如图所示,质量均为M的A、B两个物块用劲度系数为K的轻弹簧相连,竖直地静置于水平地面.此时弹簧的弹性势能为E0,现将质量也为M的物块C由A的正上方距A物块h高处由静止释放,下落后与A发生碰撞,碰后C与A立即-起向下运动,但C与A不粘连,不计空气阻力.求