题目内容
如图甲质量均为m的A、B两球间有压缩的轻短弹簧处于锁定状态，放置在水平面上竖直光滑的发射管内（两球紧靠弹簧不相连，两球的大小尺寸和弹簧尺寸都可忽略，它们整体视为质点），解除锁定后，A球能上升的最大高度为H．如图乙现让两球包括锁定的弹簧从水平面出发，沿光滑的半径为R=2H的半圆槽从左侧由静止开始下滑，滑至最低点时，瞬间解除锁定．求：（1）两球运动到最低点弹簧锁定解除前所受轨道的弹力？
（2）A球离开圆槽后能上升的最大高度？
分析：A、B系统由水平位置滑到轨道最低点，根据机械守恒定律求出最低点时速度，根据牛顿第二定律求解．
由解除锁定后的最大高度可求得弹簧的弹性势能；在圆槽底部释放时，由动量守恒结合机械能守恒定律可求得A球的速度；再由机械能守恒可求得A球上升的最大高度．
由解除锁定后的最大高度可求得弹簧的弹性势能；在圆槽底部释放时，由动量守恒结合机械能守恒定律可求得A球的速度；再由机械能守恒可求得A球上升的最大高度．
解答：解：（1）A、B系统由水平位置滑到轨道最低点时速度为v0，设半径为R，
由机械守恒定律得：2mgR=
2mv02，
设轨道对小球的弹力为F，由牛顿第二定律得：
F-2mg=2m
，解得：F=6mg；
（2）图甲中解除锁定后弹簧将弹性势能全部转化为A的机械能，
则弹性势能为EP=mgH，
图乙中滑至最低点时有：2mg×2H=
2mv02，
解除锁定后A、B的速度分别为vA、vB，
解除锁定过程中动量守恒：2mv0=mvB+mvA，
系统机械能守恒：
2mv02+EP=
m vA2+
mvB2，
有：vA2-4vA
+3gH=0，
解得：vA=3
，（或vA=
舍去）
设球A上升的高度为h，球A上升过程机械能守恒
mg（h+R）=
mvA2，解得：h=2.5H；
答：（1）两球运动到最低点弹簧锁定解除前所受轨道的弹力为6mg．
（2）A球离开圆槽后能上升的最大高度为2.5H．
由机械守恒定律得：2mgR=
| 1 |
| 2 |
设轨道对小球的弹力为F，由牛顿第二定律得：
F-2mg=2m
| ||
| R |
（2）图甲中解除锁定后弹簧将弹性势能全部转化为A的机械能，
则弹性势能为EP=mgH，
图乙中滑至最低点时有：2mg×2H=
| 1 |
| 2 |
解除锁定后A、B的速度分别为vA、vB，
解除锁定过程中动量守恒：2mv0=mvB+mvA，
系统机械能守恒：
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
有：vA2-4vA
| gH |
解得：vA=3
| gH |
| gH |
设球A上升的高度为h，球A上升过程机械能守恒
mg（h+R）=
| 1 |
| 2 |
答：（1）两球运动到最低点弹簧锁定解除前所受轨道的弹力为6mg．
（2）A球离开圆槽后能上升的最大高度为2.5H．
点评：本题考查动量守恒及机械能守恒定律的综合应用，要注意分析过程中的能量转化，并结合正确的规律求解．
练习册系列答案
相关题目
（2012?邯郸一模）如图所示，两电阻不计的足够长光滑平行金属导轨与水平面夹角为θ，导轨间距为l，所在平面的正方形区域abcd内存在有界匀强磁场，磁感应强度大小为B，方向垂直于斜面向上．如图所示，将甲、乙两阻值相同，质量均为m的相同金属杆放置在导轨上，甲金属杆处在磁场的上边界，甲、乙相距l．从静止释放两金属杆的同时，在金属杆甲上施加一个沿着导轨的外力，使甲金属杆在运动过程中始终沿导轨向下做匀加速直线运动，且加速度大小以a=gsinθ，乙金属杆刚进入磁场时做匀速运动．
如图甲、乙、丙所示，质量均为m的小球从倾角分别为θ1、θ2、θ3，但高度相同的光滑斜面顶端由静止开始下滑，若已知θ1＜θ2＜θ3，则当它们到达斜面底端时，以下分析中正确的是（ ）
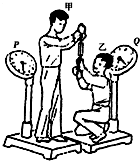如图所示，质量均为m的甲、乙两同学，分别静止于水平地面的台秤P、Q上，他们用手分别竖直牵拉一只弹簧秤的两端，稳定后弹簧秤的示数为F，若弹簧秤的质量不计，下列说法正确的是（ ）| A、甲受到的拉力大于F，乙受到的拉力小于F | B、台秤P的读数等于mg+F | C、台秤Q的读数为mg-2F | D、两台秤的读数之和为2mg |
（18分）如图甲质量均为m的A、B两球间有压缩的轻短弹簧处于锁定状态，放置在水平面上竖直光滑的发射管内（两球紧靠弹簧不相连，两球的大小尺寸和弹簧尺寸都可忽略，它们整体视为质点），解除锁定后，A球能上升的最大高度为H。如图乙现让两球包括锁定的弹簧从水平面出发，沿光滑的半径为R=2H的半圆槽从左侧由静止开始下滑，滑至最低点时，瞬间解除锁定。