题目内容
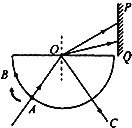
【题目】如图,ABD为竖直平面内的轨道,其中AB段是水平粗糙的、BD段为半径R=0.4m的半圆光滑轨道,两段轨道相切于B点.小球甲从C点以速度υ0沿水平轨道向右运动,与静止在B点的小球乙发生弹性碰撞.已知甲、乙两球的质量均为m,小球甲与AB段的动摩擦因数为μ=0.5,C、B距离L=1.6m,g取10m/s2 . (水平轨道足够长,甲、乙两球可视为质点)
(1)甲乙两球碰撞后,乙恰能通过轨道的最高点D,求乙在轨道上的首次落点到B点的距离;
(2)在满足(1)的条件下,求的甲的速度υ0;
(3)若甲仍以速度υ0向右运动,增大甲的质量,保持乙的质量不变,求乙在轨道上的首次落点到B点的距离范围.
【答案】
(1)
解:设乙到达最高点的速度为vD,乙离开D点到达水平轨道的时间为t,乙的落点到B点的距离为x,乙恰能通过轨道最高点,则
mg=m ![]() …①
…①
乙做平抛运动过程有:
2R= ![]() gt2…②
gt2…②
x=vDt…③
联立①②③得:x=0.8 m…④
(2)
解:设碰撞后甲、乙的速度分别为v甲、v乙,取向右为正方向,根据动量守恒定律和机械能守恒定律有
mvB=mv甲+mv乙 …⑤
![]() mvB2=
mvB2= ![]() mv甲2+
mv甲2+ ![]() mv乙2…⑥
mv乙2…⑥
联立⑤⑥得:v乙=vB⑦
对乙从B到D,由动能定理得:﹣mg2R= ![]() mv02﹣
mv02﹣ ![]() mv乙2…⑧
mv乙2…⑧
联立①⑦⑧得:vB=2 ![]() m/s…⑨
m/s…⑨
甲从C到B,由动能定理有:﹣μmgL= ![]() mvB2﹣
mvB2﹣ ![]() mv02⑨
mv02⑨
解得:v0=6m/s
(3)
解:设甲的质量为M,碰撞后甲、乙的速度分别为vM、vm,取向右为正方向,根据动量守恒定律和机械能守恒定律有:
MvB=MvM+mvm…⑩
![]() MvB2=
MvB2= ![]() MvM2+
MvM2+ ![]() mvm2
mvm2
联立得⑩(11)得:vm= ![]()
由M=m和M≥m,可得 vB≤vm<2vB
设乙球过D点时的速度为vD',由动能定理得:
﹣mg2R= ![]() mv′02﹣
mv′02﹣ ![]() mvm2
mvm2
联立⑨(13)(14)得:2 m/s≤vD'<8 m/s
设乙在水平轨道上的落点距B点的距离为x',有:x'=vD't
联立②(15)(16)得:0.8 m≤x'<3.2m
【解析】(1)乙恰能通过轨道的最高点D时,由重力提供向心力,由牛顿第二定律求得乙通过D点时的速度,再由平抛运动的规律求乙在轨道上的首次落点到B点的距离;(2)对于甲乙碰撞,根据动量守恒定律和机械能守恒定律可以知道它们交换速度.对乙从B到D,由动能定理求得碰后瞬间乙的速度.对甲从C到B,由动能定理求得速度υ0;(3)根据动量守恒定律和机械能守恒定律得到碰后乙速度的范围,再由平抛运动的规律求得乙在轨道上的首次落点到B点的距离范围.
【考点精析】本题主要考查了向心力和机械能守恒及其条件的相关知识点,需要掌握向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力;在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变才能正确解答此题.

【题目】如图所示,在探究“凸透镜成像规律”的实验中,依次将点燃的蜡烛、凸透镜、光屏放在光具座上,调节烛焰、凸透镜、光屏的中心大致在同一高度.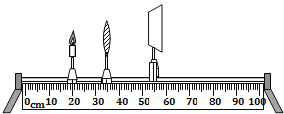
如表是小华同学实验时记录的几组数据:
实验次数 | 物距u/cm | 像距v/cm |
1 | 30 | 15 |
2 | 20 | 20 |
3 | 15 | 30 |
4 | 5 | / |
(1)第4次实验时所成像的特点是?
(2)当光屏上得到一个倒立缩小的实像时,保持透镜的位置不变,要使屏上的像变大些,应将蜡烛与透镜怎样操作?,将光屏与透镜怎样操作?
(3)第1次实验时,小华将一近视眼镜紧贴在凸透镜的前面,要在光屏上再次得到清晰的像,应将光屏向透镜方向怎样移动?