题目内容
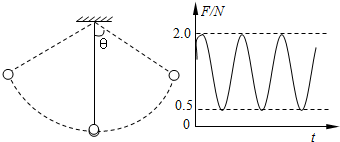
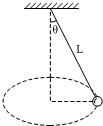在如图所示，绳子得上端固定，下端拴着一个小球，小球在水平面内做匀速圆周运动．已知绳子长度为L，绳子转动过程中与竖直方向的夹角为θ，重力加速度为g；求小球做匀速圆周运动的周期．
解：小球仅受重力和沿绳子向上的拉力，
对小球列牛顿第二定律：mgtanθ=m（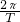
）2r
其中 r=Lsinθ
解得：T=2π
答：小球做匀速圆周运动的周期2π．
分析：小球所受的合力提供向心力，所以重力与绳子拉力的合力提供向心力，根据牛顿第二定律可解得．
点评：物体所受的合力提供其做圆周运动所需的向心力，关键物体是能解出物体所受的合外力．
对小球列牛顿第二定律：mgtanθ=m（
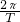）2r 其中 r=Lsinθ
解得：T=2π
答：小球做匀速圆周运动的周期2π
．分析：小球所受的合力提供向心力，所以重力与绳子拉力的合力提供向心力，根据牛顿第二定律可解得．
点评：物体所受的合力提供其做圆周运动所需的向心力，关键物体是能解出物体所受的合外力．
练习册系列答案
相关题目
