题目内容
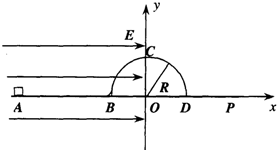 如图所示,光滑水平面上固定着一半径为R的光滑半圆柱体,半圆柱体的轴线过坐标原点O,在x<0 一侧的整个空间存在电场强度大小为E、方向水平向右的匀强电场一个质量为m、带正电荷q的小滑块,从水平面上的A点由静止释放,到达B点后沿半圆柱面继续上滑(B点处有一光滑小圆弧面连接水平面与半圆柱面),达到半圆柱面顶点C时,小滑块对半圆柱面的压力恰好为零,离开柱面后小滑块落到水平上的P点.试求:
如图所示,光滑水平面上固定着一半径为R的光滑半圆柱体,半圆柱体的轴线过坐标原点O,在x<0 一侧的整个空间存在电场强度大小为E、方向水平向右的匀强电场一个质量为m、带正电荷q的小滑块,从水平面上的A点由静止释放,到达B点后沿半圆柱面继续上滑(B点处有一光滑小圆弧面连接水平面与半圆柱面),达到半圆柱面顶点C时,小滑块对半圆柱面的压力恰好为零,离开柱面后小滑块落到水平上的P点.试求:(1)AB间的距离;
(2)BP间的距离.
分析:对AB段由动能定理即可求出AB距离;由平抛运动的知识即可顺利求出BP的距离.
解答:解:(1)设小滑块达到半圆柱面的顶点时的速度为Vc,AB间的距离为S1,由动能定理得:
Eq(S1+R)-mgR=
mVC2…①
在半圆柱面顶点C:mg=m
… ②
联立①②解得:S1=(
-1)R
(2)小滑块离开圆柱面后平抛运动,设OP间的距离为S2,离开柱面后落到水平面上的P点所需时间为t,则:
S2=VCt…③
R=
gt2…④
联立③④解得:S2=
R
故得BP间的距离为(1+
)R
答:(1)AB间的距离为(
-1)R;
(2)BP间的距离为(1+
)R.
Eq(S1+R)-mgR=
| 1 |
| 2 |
在半圆柱面顶点C:mg=m
| Vc2 |
| R |
联立①②解得:S1=(
| 3mg |
| 2Eq |
(2)小滑块离开圆柱面后平抛运动,设OP间的距离为S2,离开柱面后落到水平面上的P点所需时间为t,则:
S2=VCt…③
R=
| 1 |
| 2 |
联立③④解得:S2=
| 2 |
故得BP间的距离为(1+
| 2 |
答:(1)AB间的距离为(
| 3mg |
| 2Eq |
(2)BP间的距离为(1+
| 2 |
点评:只要掌握动能定理及其适用条件即可顺利解决此类问题.

练习册系列答案
相关题目
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
 (2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:
(2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求: 如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )
如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )