题目内容
如图所示，A、B、C、D四图中的小球以及小球所在的左侧斜面完全相同，现从同一高度h处由静止释放小球，使之进入右侧不同的轨道：除去底部一小段圆弧，A图中的轨道是一段斜面，高度大于h；B图中的轨道与A图中轨道相比只是短了一些，且斜面高度小于h；C图中的轨道是一个内径略大于小球直径的管道，其上部为直管，下部为圆弧形，与斜面相连，管的高度大于h；D图中的轨道是个半圆形轨道，其直径等于h.如果不计任何摩擦阻力和拐弯处的能量损失，小球进入右侧轨道后能到达h高度的是( )
【答案】
AC
【解析】
试题分析：根据机械能守恒定律可知，在①③中，当小球速度减小到0时，小球达到高度h，故A、C正确；在②中，小球达到轨道顶端后做斜上抛运动，小球在水平方向上不受外力，故小球达到最高点时依然有动能，故无法达到h高度，所以B错误；在④中，小球沿轨道做竖直面内的圆周运动，能通过最高点的临界速度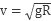
，同理知，小球无法达到h高度，所以D也错误。
考点：机械能守恒、圆周运动
练习册系列答案
相关题目
如图所示，a、b、c为电场中同一电场线上的三点，且b为ac的中点，a、c电势分别为φa=8V，φc=6V．下列叙述正确的是（ ）
如图所示，A、B、C、D是某匀强电场中的4个等势面，一个质子和一个α粒子（电荷量是质子的2倍，质量是质子的4倍）同时在A等势面从静止出发，向右运动，当到达D等势面时，下列说法正确的是（ ）
如图所示，a、b和c都是厚度均匀的平玻璃板，a和b、b和c之间的夹角都为α，一细光束由红光和蓝光组成，以入射角θ从O点射入a板，且射出c板后的两束单色光通过空气射在地面上P、Q两点，由此可知（ ）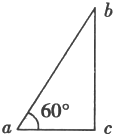
如图所示，a、b、c是匀强电场中的直角三角形的三个顶点．已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V，