题目内容
5.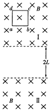 如图所示,有理想边界且范围足够大的两个水平匀强磁场Ⅰ、Ⅱ,磁感应强度均为B,两水平边界间距为2L.有一质量为m、边长为L的正方形线框abcd由粗细均匀的导线制成,总电阻为R.线框从磁场Ⅰ中某处由静止释放,运动过程中,线框平面始终与磁场方向垂直的竖直平面内,且ab边平行于磁场边界.当ab边刚离开磁场Ⅰ时,线框恰好做匀速运动;当cd边进入磁场Ⅱ前,线框又做匀速运动.求:
如图所示,有理想边界且范围足够大的两个水平匀强磁场Ⅰ、Ⅱ,磁感应强度均为B,两水平边界间距为2L.有一质量为m、边长为L的正方形线框abcd由粗细均匀的导线制成,总电阻为R.线框从磁场Ⅰ中某处由静止释放,运动过程中,线框平面始终与磁场方向垂直的竖直平面内,且ab边平行于磁场边界.当ab边刚离开磁场Ⅰ时,线框恰好做匀速运动;当cd边进入磁场Ⅱ前,线框又做匀速运动.求:(1)线框做匀速运动时,产生的感应电流的大小;
(2)线框从开始运动到完全进入磁场Ⅱ的过程中的最大速度;
(3)线框通过两磁场边界过程中产生的焦耳热.
分析 (1)线框做匀速运动时,安培力与重力平衡,由平衡条件求感应电流.
(2)当ab边刚离开磁场Ⅰ时,线框恰好做匀速运动,离开磁场后做匀加速直线运动,线圈进入磁场Ⅱ应先做减速运动,最后做匀速运动,所以线圈刚进入磁场Ⅱ时速度最大,由机械能守恒求最大速度.
(3)根据能量守恒求焦耳热.
解答 解:(1)线框做匀速运动时,安培力与重力平衡,则有
mg=BIL,I=$\frac{mg}{BL}$
(2)设线框做匀速运动时的速度为v,最大速度为vm.
由I=$\frac{E}{R}=\frac{BLv}{R}$得 v=$\frac{mgR}{{B}^{2}{L}^{2}}$
由题分析知,线圈刚进入磁场Ⅱ时速度最大,线圈从离开磁场Ⅰ到刚进入磁场Ⅱ的过程,由机械能守恒得
mgL=$\frac{1}{2}m{v}_{m}^{2}-\frac{1}{2}m{v}^{2}$
可得 vm=$\sqrt{\frac{{m}^{2}{g}^{2}{R}^{2}}{{B}^{4}{L}^{4}}+2gL}$
(3)线框通过两磁场边界过程中产生的焦耳热为
Q=mgL+(mgL+$\frac{1}{2}m{v}_{m}^{2}-\frac{1}{2}m{v}^{2}$)=3mgL
答:
(1)线框做匀速运动时,产生的感应电流的大小是$\frac{mg}{BL}$;
(2)线框从开始运动到完全进入磁场Ⅱ的过程中的最大速度是$\sqrt{\frac{{m}^{2}{g}^{2}{R}^{2}}{{B}^{4}{L}^{4}}+2gL}$;
(3)线框通过两磁场边界过程中产生的焦耳热是3mgL.
点评 分析清楚线框的运动过程,正确分析能量如何转化是两个关键,再应用E=BLv、欧姆定律等规律即可正确解题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
9.如图是某物体做直线运动的v-t图象,下列有关物体运动情况判断正确的是( )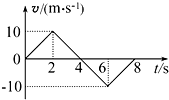

| A. | 3s末物体的加速度大小为5 m/s2 | B. | 4s末物体回到出发点 | ||
| C. | 6s末物体的速度最大 | D. | 4s末物体的加速度为零 |
10.关于速度、速度变化量和加速度,正确的说法是( )
| A. | 物体运动的速度改变量越大,它的加速度一定越大 | |
| B. | 速度很大的物体,其加速度可以很小,可以为零 | |
| C. | 某时刻物体速度为零,其加速度可能很大 | |
| D. | 加速度很大时,运动物体的速度一定变化很快 |
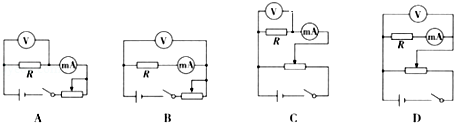
13.某学习小组为探究导电溶液的电阻在体积相同时,电阻值与长度的关系.选取了一根乳胶管,里面灌满了盐水,两端用粗铜丝塞住管口,形成一段封闭的盐水柱.进行了如下实验:
(1)该小组将盐水柱作为纯电阻,粗测其电阻约为几千欧.现采用伏安法测盐水柱的电阻,有如下实验器材供选择:
A.直流电源:电动势12V,内阻很小,额定电流为1A;
B.电流表A1:量程0~10mA,内阻约10Ω;
C.电流表A2:量程0~600mA,内阻约0.5Ω;
D.电压表V:量程0~15V,内阻约15kΩ;
E.滑动变阻器R1:最大阻值10Ω,额定电流为1A;
F.滑动变阻器R2:最大阻值15kΩ;额定电流为100mA
G.开关、导线等
在可供选择的器材中,应选用的电流表是A1(填“A1”或“A2”),应该选用的滑动变阻器是R2(填“R1”或“R2”).
(2)该小组已经完成部分导线的连接,请你在实物接线图1中完成余下导线的连接.
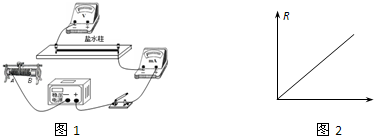
(3)握住乳胶管的两端把它均匀拉长,多次实验测得盐水柱长度L、电阻R的数据如表:
为了研究电阻R与长度L的关系,该小组用纵坐标表示电阻R,作出了如图2所示的图线,你认为横坐标表示的物理量是L2.
(1)该小组将盐水柱作为纯电阻,粗测其电阻约为几千欧.现采用伏安法测盐水柱的电阻,有如下实验器材供选择:
A.直流电源:电动势12V,内阻很小,额定电流为1A;
B.电流表A1:量程0~10mA,内阻约10Ω;
C.电流表A2:量程0~600mA,内阻约0.5Ω;
D.电压表V:量程0~15V,内阻约15kΩ;
E.滑动变阻器R1:最大阻值10Ω,额定电流为1A;
F.滑动变阻器R2:最大阻值15kΩ;额定电流为100mA
G.开关、导线等
在可供选择的器材中,应选用的电流表是A1(填“A1”或“A2”),应该选用的滑动变阻器是R2(填“R1”或“R2”).
(2)该小组已经完成部分导线的连接,请你在实物接线图1中完成余下导线的连接.

(3)握住乳胶管的两端把它均匀拉长,多次实验测得盐水柱长度L、电阻R的数据如表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 长度L(cm) | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 | 45.0 |
| 电阻R(kΩ) | 1.3 | 2.1 | 3.0 | 4.1 | 5.3 | 6.7 |
20.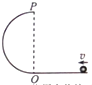 如图所示,半径为R的半圆轨道固定在竖直平面内,且与水平轨道相切于O点,质量为m的小球沿水平轨道向左运动通过O点进入半圆轨道后恰能通过最高点P,小球离开P点后落回水平轨道,不计一切阻力,重力加速度为g,下列说法正确的是( )
如图所示,半径为R的半圆轨道固定在竖直平面内,且与水平轨道相切于O点,质量为m的小球沿水平轨道向左运动通过O点进入半圆轨道后恰能通过最高点P,小球离开P点后落回水平轨道,不计一切阻力,重力加速度为g,下列说法正确的是( )
 如图所示,半径为R的半圆轨道固定在竖直平面内,且与水平轨道相切于O点,质量为m的小球沿水平轨道向左运动通过O点进入半圆轨道后恰能通过最高点P,小球离开P点后落回水平轨道,不计一切阻力,重力加速度为g,下列说法正确的是( )
如图所示,半径为R的半圆轨道固定在竖直平面内,且与水平轨道相切于O点,质量为m的小球沿水平轨道向左运动通过O点进入半圆轨道后恰能通过最高点P,小球离开P点后落回水平轨道,不计一切阻力,重力加速度为g,下列说法正确的是( )| A. | 小球落地点离O点的水平距离为$\sqrt{2}$R | B. | 小球落地点离O点的水平距离为2R | ||
| C. | 小球落地时的动能为2mgR | D. | 小球落地时的动能为2.5mgR |
17.有两个匀强磁场区域 I和 II,I中的磁感应强度是 II中的k倍,两个速率相同的电子分别在两磁场区域做圆周运动.与 I中运动的电子相比,II中的电子( )
| A. | 运动轨迹的半径是I中的k倍 | B. | 加速度的大小是I中的k倍 | ||
| C. | 做圆周运动的周期是I中的k倍 | D. | 做圆周运动的角速度是Ⅰ中的k倍 |
15.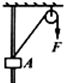 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则下列说法正确的是( )
 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则下列说法正确的是( )| A. | 拉力F变小 | B. | 杆对A的弹力FN不变 | ||
| C. | 拉力F的功率P不变 | D. | 绳子自由端的速率v增大 |