题目内容
20．
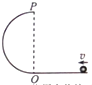如图所示，半径为R的半圆轨道固定在竖直平面内，且与水平轨道相切于O点，质量为m的小球沿水平轨道向左运动通过O点进入半圆轨道后恰能通过最高点P，小球离开P点后落回水平轨道，不计一切阻力，重力加速度为g，下列说法正确的是（ ）| A． | 小球落地点离O点的水平距离为$\sqrt{2}$R | B． | 小球落地点离O点的水平距离为2R | ||
| C． | 小球落地时的动能为2mgR | D． | 小球落地时的动能为2.5mgR |
分析 小球恰能通过半圆弧轨道的最高点P时，由重力提供向心力，求出小球通过P点时的速度．小球通过P点后做平抛运动，由高度2R求出时间，再由x=v0t求出水平距离．根据机械能守恒定律求出小球落地点时的动能．
解答 解：A、小球恰能通过半圆弧轨道的最高点P时，重力提供向心力，由牛顿第二定律得：mg=m$\frac{{v}^{2}}{R}$，解得：v=$\sqrt{gR}$，小球离开P点后平抛运动，竖直方向：2R=$\frac{1}{2}$gt2，水平方向：x=vt，解得：x=2R，故A错误，B正确．
C、小球从离开P到落地过程机械能守恒，由机械能守恒定律得：Ek=mg•2R+$\frac{1}{2}$mv2，=2.5mgR，故C错误，D正确；
故选：BD．
点评 本题是一道力学综合题，分析清楚小球运动过程是正确解题的关键，解题时要注意小球做圆周运动的临界条件，应用牛顿第二定律、机械能守恒定律、平抛运动规律可以解题．
练习册系列答案
相关题目
4．
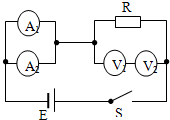四个相同的电流表分别改装成两个电流表A1、A2和两个电压表 V1、V2，A1的量程大于A2的量程，V1的量程大于V2的量程，把它们接入如图所示的电路，闭合开关后（ ）
四个相同的电流表分别改装成两个电流表A1、A2和两个电压表 V1、V2，A1的量程大于A2的量程，V1的量程大于V2的量程，把它们接入如图所示的电路，闭合开关后（ ）| A． | A1的读数比A2的读数小 | |
| B． | A1指针偏转角度与A2指针偏转角度相等 | |
| C． | V1读数比V2读数大 | |
| D． | V1指针偏转角度与V2指针偏转角度不等 |
如图，在光滑水平面上有A，B两带电小球，A质量m1，带正电q1，B质量m2，带负电量q2，用一水平力拉A，使AB保持L的距离一起向前运动，拉力F为多大？
15．地球表面附近某区域存在大小为 150N/C、方向竖直向下的电场．一质量为1.00×10-4kg、带电量为-1.00×10-7 C的小球从静止释放，在电场区域内下落 10.0m．对此过程，该小球的电势能和动能的改变量分别为（重力加速度大小取10m/s2，忽略空气阻力）（ ）
| A． | -1.50×10-4 J和9.65×10-3 J | B． | 1.50×10-4 J和9.65×10-3 J | ||
| C． | -1.50×10-4 J和9.5×10-3 J | D． | 1.50×10-4 J和9.5×10-3 J |
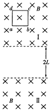如图所示，有理想边界且范围足够大的两个水平匀强磁场Ⅰ、Ⅱ，磁感应强度均为B，两水平边界间距为2L．有一质量为m、边长为L的正方形线框abcd由粗细均匀的导线制成，总电阻为R．线框从磁场Ⅰ中某处由静止释放，运动过程中，线框平面始终与磁场方向垂直的竖直平面内，且ab边平行于磁场边界．当ab边刚离开磁场Ⅰ时，线框恰好做匀速运动；当cd边进入磁场Ⅱ前，线框又做匀速运动．求：
（1）动能相等的两人造地球卫星A、B的轨道半径之比RA：RB=1：2，它们的角速度之比ωA：ωB=2$\sqrt{2}$：1，质量之比mA：mB=1：2．
10．
甲、乙两辆汽车在平直的公路上同一地点沿相同方向由静止开始做直线运动，它们运动的加 速度随时间变化a-t图象如图所示．关于甲、乙两车在0～20s的运动情况，下列说法正确的是（ ）
甲、乙两辆汽车在平直的公路上同一地点沿相同方向由静止开始做直线运动，它们运动的加 速度随时间变化a-t图象如图所示．关于甲、乙两车在0～20s的运动情况，下列说法正确的是（ ）| A． | 在t=10s时两车相遇 | B． | 在t=20s时两车相遇 | ||
| C． | 在t=10s时两车相距最远 | D． | 在t=20s时两车相距最远 |