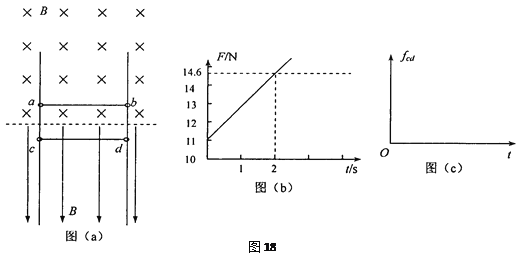
题目内容
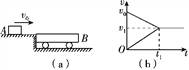
【题目】某实验小组利用如图甲所示的实验装置来探究做功与物体动能变化的关系,当地的重力加速度为g。
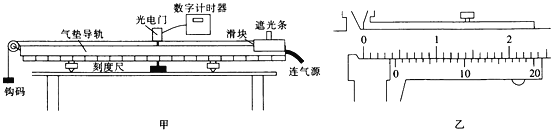
(1)该小组成员用游标卡尺测量遮光条的宽度d,如图乙所示,则d=_________cm,用天平测得滑块与遮光条的总质量为M,钩码的质量为m。
(2)实验前调节气垫导轨使之水平,实验时将滑块从图示位置由静止释放,由数字计时器读出遮光条通过光电门的时间Δt=1.0×10-2 s,则滑块经过光电门时的瞬时速度v=____m/s(结果保留两位有效数字)。
(3)在本实验中为了确保细线拉力所做的功与钩码重力所做的功近似相等,则滑块与遮光条的总质量M与钩码的质量m间的关系应满足M_________(填“”“”或“=”)m。
(4)本实验中还需要测量的物理量是:___________________________________________。
【答案】0.430 0.43 滑块释放时遮光条到光电门的距离x
【解析】
(1)根据游标卡尺的读数方法读出游标卡尺的读数;
(2)遮光条较窄,认为匀速穿过光电门,根据v=d/△t得出瞬时速度;
(3)根据牛顿第二定律求出细线拉力的表达式,据此作答;
(4)根据细线拉力做的功为W=mgx,据此作答。
(1)由游标卡尺的读数规则可得遮光条的宽度为d=4mm+0.05×6mm=4.30mm=0.430cm;
(2)滑块经过光电门时的瞬时速度为v=d/△t=(0.430×102)/1.0×102m/s=0.43m/s;
(3)令细线拉力为T,则有T=Ma及mg-T=ma,T=![]() ,
,
所以只有满足M>>m时,细线拉力才近似等于钩码重力,细线拉力所做的功与钩码重力做的功才近似相等;
(4)细线拉力做的功为W=mgx,即需要测定滑块上的遮光条的初位置到光电门的距离x;

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目