题目内容
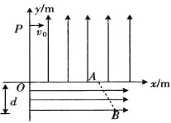
【题目】在如图所示的平面直角坐标系xOy中，第Ⅰ象限区域内有沿y轴正方向（竖直向上）的匀强电场，电场强度大小E0＝50 N/C；第Ⅳ象限区域内有一宽度d＝0.2 m、方向沿x轴正方向（水平向右）的匀强电场。质量m＝0.1 kg、带电荷量q＝+1×10-2C的小球从y轴上P点以一定的初速度垂直y轴方向进入电场，通过第Ⅰ象限后，从x轴上的A点进入第Ⅳ象限，并恰好沿直线通过该区域后从B点离开，已知P、A的坐标分别为(0，0，4)，(0，4，0)，取重力加速度g＝10 m/s2。求：
（1）初速度v0的大小；
（2）A、B两点间的电势差UAB；
（3）小球经过B点时的速度大小。
【答案】（1）1 m/s （2）5 V （3）
【解析】
（1）小球进入竖直方向的匀强电场后做类平抛运动，水平方向做匀速运动，竖直方向都做匀加速运动，分别列位移方程，即可求解；
（2）小球在第四象限恰好做直线运动，合外力的方向与速度方向在一条直线上，根据
可求电场强度，根据U＝El可求A、B间的电势差；
（3）对小球运动的全过程，由动能定理，可求小球经过B点时的速度大小。
（1）小球进入竖直方向的匀强电场后做类平抛运动，小球带正电，受到的电场力竖直向上，根据牛顿第二定律，加速度
解得a＝5 m/s2
根据平抛运动规律有，小球沿水平方向做匀速运动：xA＝v0t
沿竖直方向有：
解得v0＝1 m/s。
（2）设水平电场的电场强度大小为E，因未进入电场前，带电小球做类平抛运动，所以进入电场时竖直方向的速度
因为小球在该电场区域恰好做直线运动，所以合外力的方向与速度方向在一条直线上，即速度方向与合外力的方向相同，有
解得E＝50 N/C
设小球在水平电场中运动的水平距离为l
根据U＝El
解得UAB＝5 V。
（3）设小球在B点的速度大小为v，对小球运动的全过程，由动能定理，有
解得
。
